множества, меньшие пустого; квантовые множества; пустое пространство; однородность пространства; структура без элементов; взаимодействие разума и реальности; эффективность математики.
В этом тексте я попытаюсь изложить несколько довольно безумных идей.
Также смотри
добавления (ниже на этой же страничке).
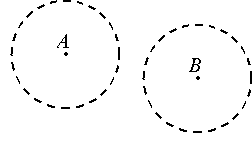1. Идея, вытекающая из однородности пространства. Рассмотрим две точки нашего
пространства. Известно, что они обладают изометричными окрестностями. О чем может говорить эта изометричность? Эта изометричность может говорить о том, что эти области - суть одно и тоже. То есть пространство рядом с точкой
A и пространство рядом с точкой
B - это одно и то же простран
ство (см. рисунок). Предположение может показаться диким, оно не совсем понятно, но в дальнейшем смысл его будет уточняться, а пока удовлетворимся этим. Эти две окрестности похожи на двое точных часов, которые идут синхронно; можно считать, что причина синхронности в том, что они показывают одно и то же время. Также (повторяюсь, потому что считаю нужным) и с пространством, окружающим точки: пространство, окружающее точку
A, и пространство, окружающее точку
B, – это одно и то же пространство.
2. Множества(?) меньшие пустого. Эта идея присоединяется к первой, появилась она независимо(?), связана с определением порядкового числа по Нейману
(см. статью Неймана), именно поэтому статья Неймана и лежит на моем сайте (только читать ее нужно умеючи). Итак:
Пусть даны несколько элементов
a1, a2, a3, a4, . . . , an. При использовании стандартных обозначений теории множеств, множество
A, образованное из
элементов a1, a2, a3, a4, . . . , an, записывается следующим образом:
A = {a1, a2, a3, a4, . . . , an}. Далее мы будем использовать эти обозначения. Используя стандартные обозначения мы можем написать, например, такую совокупность значков }
{, или такую }
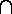
{. (Не следует недооценивать значков, значки – это важно, это не просто техническое средство, они позволяют думать.) Так вот, если рассматривать такие совокупности значков как цельные значки, обозначающие некие сущности, то эти сущности будут обладать интересными свойствами.
Например, попробуем образовать из }
{ одноэлементное множество. Получаем
{}{} = Ø. Как можно проинтерпретировать это свойство? В связи с этим свойством имеется одна трудность. Заключается она в том, что, вероятно, назвать сущности типа
}{ подходящим образом не удастся. Имена для этих сущностей будут вести себя не так, как эти сущности: из имени мы можем сделать одноэлементное множество, а из сущности типа
}{ – нет. Вообще-то сущности
типа }{ неправильно, наверное, называть множествами или сущностями или объектами или обращаться к ним с помощью местоимений; но поскольку подходящих слов нет, то я называю их “объектами
типа }{”. За последнее предложение меня можно упрекнуть в парадоксальности («...называю то, что невозможно назвать...»), но по другому я пока не могу, так что пока придется мириться с этими парадоксами.
Еще одно свойство. Пусть
A – любой объект. Образуем из него одноэлементное множество {
A}. Имеем:
{}{} = Ø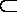
{A} т.е. }{ 
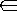{A}, для любого объекта A. И вот это свойство интересно тем, что объекты типа
}{ оказываются присущи любому объекту, любой материальной точке (ср. с тем, что философы говорят о неотделимости пространства от материи и о всеобщности пространства, см.
цитатку). Также проясняется смысл того, что сказано об одинаковости двух окрестностей, т.е. если пространство “сделано” из объектов типа
}{, то оно будет однородным, т.к. если объекты типа
}{ присущи точке
A, то они будут присущи и
точке B.
3. Что значит “обратить внимание”? Слова “обратить внимание” мы будем понимать как “образовать множество”. Такое понимание слов “обратить внимание” несколько расходится с тем смыслом, который мы обычно вкладываем в эти слова. Наше понимание слов “обратить внимание” беднее общепринятого. Но так и должно быть при всяком упрощении; удачно ли такое упрощение и, если удачно, то насколько – сейчас трудно сказать.
При таком понимании слов “обратить внимание” получается, что объекты типа
}{ разрушаются если мы пытаемся обратить на них внимание.
Или, если смотреть шире, объекты типа
}{ взаимодействуют с разумом. (Если разум сможет непосредственно влиять на реальность, то возникнут очень интересные вопросы.)
Объяснить почему такое понимание правильно – я не могу. Сопоставьте предложенное мной понимание слов “обратить внимание” с “определением” множества (Кантор, Хаусдорф), согласно которому множество есть многое, мыслимое как единое. Понимается это “определение” (Хаусдорф) как указание на
психический акт, который может быть нельзя, а может не нужно, разлагать на более простые. Посредством этого акта мы
мысленно объединяем некоторые элементы и с тем, что получилось в результате объединения, начинаем обращаться как с целым.
Такое понимание слов “обратить внимание” направлено на то, чтобы хоть как-то привязать объекты типа
}{ к интуиции. Можно было попробовать начать мыслить формально, т.е. начать выписывать различные комбинации значков не вдаваясь поначалу в их смысл, но я плохо умею это делать и не считаю нужным это делать; мы уже один раз поигрались со значками (когда написали совокупность значков
}{ ), теперь нужно придать этим значкам смысл. А поскольку при получении комбинации значков
}{ мы отправлялись от теоретико-множественных записей, то и интерпретация должна быть связана с теорией множеств. Однако интерпретация в привычном смысле вряд ли возможна. Остается, как мне кажется, только перечитывать “определение” множества и делать с объектами типа
}{ нечто подобное, т.е. говорить как объекты типа
}{ связаны с нашим разумом.
Возвращаясь к пространству можно сказать теперь, что если пространство “сделано” из объектов типа
}{, то для нас оно будет пустым, оно не состоит не из каких элементов.
4. Дальнейшие действия. На чем я остановился. Основным препятствием является невозможность обратить внимание на объект типа
}{. Но есть одна зацепка, а именно: поскольку объекты типа
}{ присущи любому объекту, то они присущи и нашему разуму (можно предположить, что эти объекты не только “образуют” пространство, в котором существует мозг, но проявляют себя и еще каким-то образом). Может быть они проявляют себя каким-то малозаметным образом и надо только постараться их увидеть? Сейчас я пытаюсь понять, как вообще взяться за это дело. Сделать сразу, «захотел и сделал» – не получится; сходу тут не сделаешь, нужна методика, нужно сильное воздействие на мозг (крыша бы только не съехала); а вообще я не верю, что привычными средствами, рассуждая так, как мы привыкли, можно добиться чего-то по-настоящему нового (потому что по-настоящему новое должно содержать элементы, которые не выводятся из уже известного).
Из философского словаря.
ВРЕМЯ И ПРОСТРАНСТВО – осн. формы существования материи. Философию прежде всего интересует вопрос об отношении В. и П. к материи, т.е. являются ли В. и п. реальными или это чистые абстракции, существующие только в сознании. Философы-идеалисты отрицают зависимость В. и п. от материи и рассматривают их то как формы индивидуального сознания
(Беркли, Юм , Мах), то как априорные формы чувственного созерцания
(Кант), то как категории абсолютного духа
(Гегель). Материализм подчеркивает объективный характер В. и п. В том, что В. и п. неотделимы от материи проявляется их универсальность и всеобщность.
назад к тексту
Ну и напоследок: Кому захочется что-нибудь сказать по этому тексту – пишите
на мыло (bbi-math@narod.ru).
