Об аксиомах движения



Бурцев Б.И. AA.Движущаяся точка обычно описывается с помощью функции x(t), которая каждому моменту времени t ставит в соответствие координаты движущейся точки. Если время (которое нам показывают часы) движется, т.е. показания часов меняются, то имея одно движение, движение по оси t, мы можем получить другое движение, движение точки в пространстве X, описываемое функцией x(t). Такое описание, восходящее к Галилею и Ньютону, представляется вполне удовлетворительным, тем не менее интересно было бы попытаться описать движение непосредственно, не сводя его к движению по оси t.
AB.Подчеркнем, что: сама функция вещь неподвижная, график ее неподвижная вещь, тем не менее она описывает движение. Каким образом? Мы, вслед за Галилеем, выделяем один вид движения - равномерное движение по прямой - считаем его элементарным и, используя его, описываем другое движение. те, кто не особенно интересовался этими вопросами могут посмотреть комментарии(откроется в новом окне) Далее мы будем не то чтобы подражать классикам, мы попытаемся пустить в ход те силы, которые ими двигали (попробуйте это увидеть); как бы малы эти силы ни были, возникнет некоторое понимание.
AC.Формулировка задачи представляется противоречивой, т.к. утверждения, которыми мы собираемся описывать движущуюся точку, статичны и работа не остановилась только потому, что была надежда вытеснить противоречие куда-то в другое место, хорошо бы за пределы теории. Хотя движение и время все равно должны в какой-то форме, неявной, может быть, присутствовать в высказываниях описывающих движение.
AD.Мы не будем описывать движение вообще, рассмотрим только простой случай, в котором по прямой R равномерно движется вправо точка M. Кроме того имеется наблюдатель, который за этой точкой наблюдает и фиксирует результаты наблюдений. Случай все равно интересный, потому что прямая с равномерно движущейся по ней точкой может быть использована как часы.
AE.Мы попробуем избавиться от времени в нашем описании движения. Вместо времени у нас будут особые отношения между процессом и наблюдателем. которые обеспечивают движение. Еще раз отметим, что обычное описание процессов просто упорядочивает события, говоря какое из них раньше, а какое позже, движение же отсутствует и появляется только как результат движения времени.
AF.Для того, чтобы избавиться от времени воспользуемся тем фактом, что любой процесс не мгновенен. На все требуется время.
В ЧАСТНОСТИ
AG.Время требуется на восприятие и на переход от одного восприятия к другому. Т.е., как только мы нечто восприняли, нам, вообще говоря, предъявляется для восприятия нечто другое и мы можем, сравнив воспринятое и предъявленное, осознать, что нечто изменилось. Мы можем осознать изменение, можем воспринять движущийся объект именно как движущийся  [замечание AG].
AH.Наше мышление тоже не свободно от времени. Переход от одного мысленного образа к другому требует времени. В этом сходство мышления с движущимся объектом и поэтому мы можем представлять движущиеся объекты, думать о них.
AJ.Время требуется на то, чтобы записать утверждение, которое описывает положение точки в данный момент времени и перейти от одного описания к другому. В этом сходство фиксации с мышлением и этим мы воспользуемся для описания движения.
AI.Наблюдатель, с помощью которого мы будем строить описание, будет идеальным в том смысле, что на восприятие и фиксацию результатов наблюдений ему не требуется времени, он воспринимает и фиксирует мгновенно, время ему требуется только на переход от одного наблюдения к другому и на переход от записи одного утверждения, описывающего положение точки, к записи другого утверждения.
AK.Рассмотрим утверждения, описывающие координаты движущейся точки (напоминаю: точка M равномерно движется вправо).
AL.Пусть при каком-то наблюдении координата движущейся точки описывается утверждением

_____(1)           ,
здесь m - координата движущейся точки (которая меняется), x0 - действительное число (неподвижная точка на оси).
_____Тогда другое утверждение, описывающее положение точки M, будет таким

_____(2)             (т.к. точка сместилась)   
Если мы не хотим быть связаны этим другим наблюдением, то мы можем записать его результат таким образом
     (3)           .     
AN. Связь (логическая!) между двумя наблюдениями выразится следующей формулой
Добавление к абзацу AN
Добавлено 12.03.2003
Когда мы употребляем слово "логический", то имеем в виду, что формула (4) справедлива для любого наблюдателя, каким бы он ни был. Существуют ли наблюдатели смотрящие на нашу вселенную извне и не подчиняющиеся ходу времени мы не обсуждаем.
     Эти рассуждения можно провести для любой точки x, поэтому будет справедлива следующая формула

см. комментарии+методика(откроется в новом окне)
AO.Эта формула кажется противоречивой, но к противоречию можно относиться как к факту речи (реальность не противоречива), который порождается несовершенством (принципиальным несовершенством, с которым мы боремся) языка: несоответствием между языком, статичностью его высказываний, и тем объектом, движущейся точкой, к которому этот язык применяется. Учитывая противоречие мы им, в какой-то степени, пользуемся.
AP.Заметим, что для нашей точки обратная импликация в формуле (5) места не имеет, те эта формула не совсем противоречие и, как надеется автор, при правильном использовании доказать с ее помощью все, что угодно не удастся.
AR. Теперь мы сформулируем некоторое свойство, которое нам понадобится в дальнейшем. Автор затрудняется дать ему какое-то название, которое точно отражало бы его смысл (причина, видимо в том, на обычном языке это свойство даже и не сформулируешь; впрочем, читатель может попробовать сформулировать его на обычном языке и дать ему подходящее название).
Свойство 1. Пусть наблюдатель написал две формулы:
      (6)     
      (7)     
и пусть y1>x1. Тогда y2>x2 (см. рисунки 1,2)
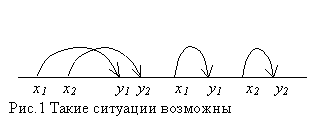
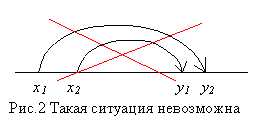  [замечание AR].
 Добавлено 12.03.2003 по результатам обсуждения (довольно квелого) на форуме Scientific.ru 25.01.2003; не знаю, имею ли я право вставлять ссылку, поэтому даю только URL:
http://www.scientific.ru/cgi-bin/dforum/forum.pl?forum=altern&id=1043486689

Стрелки на рис.1. не говорят о том, что точка "прыгает" по прямой. Эти картинки не более чем иллюстрация к формулам. Точка у нас скользит, как ей и положено, "прыжок" возникает в записи, при переходе от одного наблюдения к другому. Беда в том, что формулы дискретны

(m=x1)=>(m = x2) ("=>" обозначает импликацию и этой импликации соответствует стрелка с началом в x1 и концом в x2)

На прямой x1 отделено от x2, отсюда "скачок" в записи Рисунок этот показывает связь между двумя формулами

1.(m=x1)=>(m = x2)
2.(m=y1)=>(m = y2)

обе формулы относятся к одной и той же движущейся точке.(Подобные же замечания относятся и к остальным рисункам)
AS. Поясним что мы имеем в виду, когда говорим о статичности утверждений. Пусть дано какое-то утверждение. Мы можем обратить на него внимание, воспринять его, зафиксировать то, что мы восприняли. Утверждение будем считать статичным тогда и только тогда, когда при любом другом обращении внимания мы воспримем и зафиксируем тоже самое, что и в первый раз.
AT. С помощью формулы (5) нам удается, опираясь на статичные высказывания, сказать нечто о движении. Понятно, что для описания движения этого не достаточно. Ничто, например, не мешает нашей точке при своем движении:
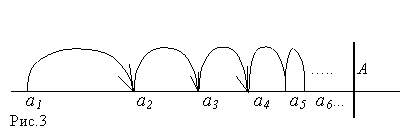
     1) приближаться к некоторому пределу не переходя его (см.рисунок) или
     2) пропускать некоторые точки прямой.
     Чтобы избежать возможности 1) достаточно потребовать выполнения следующего условия:

      ........(8)

AU. Лемма. Пусть выполнено свойство 1 и пусть выполнено условие (8). Тогда точка неограничено движется вправо.
Доказательство. (должно же быть хоть одно доказательство.)Пусть наблюдатель записал некоторую цепочку формул:

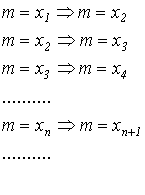
____Пусть некоторая точка x лежит левее точки A. Разумно считать, что x>a1; тогда x лежит в одном из сегментов [an, an+1]. Точка движется, поэтому наш наблюдатель может для нее записать (m=x)=>(m=x1). В силу свойства (1) точка x1 лежит в сегменте [an+1,  an+2],    an+2 < A. В силу произвольности выбора точки x мы можем утверждать, что:

Получили противоречие с условием (8). Доказательство закончено. (автор считает, что в данном случае доказательством от противного пользоваться можно, несмотря на то, что противоречия у нас получили право на существование)

AV.  Для того, чтобы движущаяся точка при своем движении не пропускала точек лежащих на прямой, потребуем чтобы переход от точки к точке происходил непрерывно. Заметим, что среди высказываний о точках прямой R, которые может сделать наш наблюдатель, существуют высказывания такие, что для них справедливо P(x)=>P(x). Вспомнив про время, об этих высказываниях можно сказать следующее: если они становятся истинными в некоторый момент времени, то они остаются истинными и во все последующие моменты. (Происходит естественная вещь: если противоречие получает право на существование, то и тавтология перестает быть простым повторением одного и того же.)
AW. Тогда тот факт, что движение точки m не ограничено и при своем движении она не пропускает точек выразится следующей группой аксиом (весьма похожих на аксиомы математической индукции).


AX. Описать равномерность не удается без привлечения метрических свойств. Автор не стал этого делать.

____ЗАКЛЮЧЕНИЕ

AY. Кому-то сделанного покажется мало. Многим сделанное покажется недостаточно логичным. прошу читателя не забывать, что у нас нет понятий, на которых мы могли бы изложить нечто. Эта работа есть попытка выработать такие понятия. Выработка понятий и языка процесс долгий, один человек, как правило, не может создать язык. Чтобы показать сложности при выработке новых понятий, всего один:
Пример. Из определения функции.
...2. Переменное количество есть количество неопределенное или всеобщее, которое содержит в себе решительно все определенные значения.
Слова эти написаны Эйлером. Видим, что когда понятия не выработаны, то даже сильные умы вынуждены продираться через свою собственную неточность (фактически он ведь о множестве говорит). Так что судить о новых вещах надо осторожно.
AZ. Нет доказательств, хотя есть некие неформальные рассуждения в абзацах AD-AN. Есть некий общий подход, напоминающий вывернутый "антропный принцип". "Антропный принцип" - мир таков, потому что в нем существуют наблюдатели (мы) с такими-то и такими-то свойствами; если бы мир был другой, то наблюдателей (в той форме, в какой они есть) не было бы. У нас - мы есть часть этого мира, у этого мира такие-то и такие-то свойства, поэтому наше описание вот такое. (Сам себя не похвалишь, ни одна собака не похвалит)

BA. Вопрос: относительно чего движется время? После этого текста можно ответить: время движется относительно наших воспоминаний, оно постоянно уходит вперед(?) от того, что мы восприняли и запомнили.




ЗАМЕЧАНИЯ

AG Следует заметить, что дело с восприятием движения обстоит не так просто. Дело в том, что сетчатка нашего глаза передает в мозг не уровень освещенности отдельных участков, а изменения этой освещенности. То есть: глаз, уже начиная с сетчатки, способен отличать движущиеся предметы от неподвижных.[назад к абзацу AG]

AR Может быть в каких-то случаях свойство (1) и нарушается; в некоторых статьях по квантовой механике рассматривается возможность нарушения причинности, мы можем представить, что при
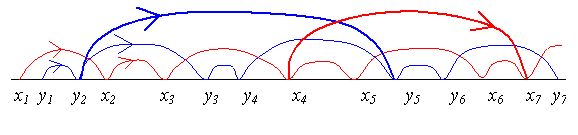
описании движения точки наблюдателем возникнет, например, такая ситуация (см рисунок). На этом рисунке в малом масштабе свойство (1) не выполняется, согласно этому свойству, если y1>x1, то y2 должно быть больше чем x2, что в данном случае не выполнено; однако если мы посмотрим в более крупном масштабе, например, на точки y2, x4, y5, x7, то свойство (1) будет выполняться.
____В работе рассматривается обычное движение и такие возможности исключаются. (Кстати: возможность нарисовать и истолковать подобную картинку может говорить о силе построений?)
[назад к абзацу AR]
Hosted by uCoz