AA.The following theory of symbolic logic recommended itself to me in the first instance by its ability to solve certain contradictions, of which the one best known to mathematicians is Burali-FortiТs concerning the greatest ordinal (see AH). But the theory in question seems not wholly dependent on this indirect recommendation; it has also, if I am not mistaken, a certain consonance with common sense which make it inherently credible. This, however, is not a merit upon which much stress should be laid; for common sense is far more fallible than it likes to believe. Ishall therefore begin by stating some of the contradictions to be solved, and shall then show how the theory of logical types effects their solution.

I.

The Contradictions.


AB.(1) The oldest contradiction of the kind in question is the Epimenides. Epimenides the Cretan said that all Cretans were liars, and all other statements made by Cretans were certainly lies. Was this a lie? The simplest form of this contradiction is afforded by the man who says УI am lying;Ф if he is lying, he is speaking the truth, and vice versa.
AC.(2) Let w be the class of all those classes which are not members of themselves. Then, whatever class x may be, Уx is a wФ is equivalent¹) to Уx is not an x.Ф Hence, giving to x the value w, Уw is a wФ is equivalent to Уw is not a w.Ф
AD.(3) Let T be the relation which subsists between two relations R and S whenever R does not have the relation R to S. Then, whatever relations R and S may be, УR has the relation T to SФ is equivalent to УR does not have the relation R to S.Ф Hence, giving the value T to both R and S, УT has the relation T to TФ is equivalent to УT does not have the relation T to T.Ф
AE.(4) The number of syllables in the English names of finite integers tends to increase as the integer grow larger, and must gradually increase indefinitely, since only a finite number of names can be made with a given finite number of syllables. Hence the names of some integers must consist of at least nineteen syllables, and among these there must be a least. Hence Уthe least integer not nameable in fewer than nineteen syllablesФ must denote a definite integer; in fact, it denotes 111 777. But Уthe least integer not nameable in fewer than nineteen syllablesФ is itself a name consisting of eighteen syllables; hence the least integer not nameable in fewer than nineteen syllables can be named in eighteen syllables, which is a contradiction.²)
AF.(5)Among transfinite ordinals some can be defined, while others cannot; for the total number of possible definition is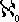 , while the number of transfinite ordinals exceeds 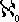. Hence there must be indefinable ordinals, and among these there must be a least. But this is defined as "the least indefinable ordinal,Ф which is a contradiction.³)
AG.(6) RichardТs paradox⁴) is akin to that of the least indefinable ordinal. It is as follows: Consider all decimals that can be defined by means of a finite number of words; let E be the class of such decimals. Then E has 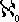terms; hence its members can be ordered as the 1st, 2nd, 3rd,Е. Let N be a number defined as follows: If the nth figure in the nth decimal is p, let the nth figure in N be p+1 (or 0, if p = 9). Then N is different from all the members of E, since, whatever finite value n may have, the nth figure in N is different from the nth figure in the nth of the decimals composing E, and therefore N is different from the nth decimal. Nevertheless we have defined N in a finite number of words, and therefore N ought to be a member of E. Thus N both is and is not a member of E.
AH.(7) Burali-FortiТs contradiction⁵) may be stated as follows: It can be shown that every well-ordered series has an ordinal number, that the series of ordinals up to and including any given ordinal exceeds the given ordinal by one, and (on certain very natural assumptions) that the series of all ordinals (in order of magnitude) is well-ordered. It follows that the series of all ordinals has an ordinal number, Ω say. But in that case the series of all ordinals including Ω has the ordinal number Ω +1, which must be greater than Ω. Hence Ω is not the ordinal number of all ordinals.
AI.In all the above contradictions (which are merely selections from an indefinite number) there is a common characteristic, which we may describe as self-reference or reflexiveness. The remark of Epimenides must include itself in its own scope. If all classes, provided they are not members of themselves, are members of w, this must also apply to w; and similarly for the analogous relational contradiction. In the cases of names and definitions, the paradoxes result from considering non-nameability and indefinability as elements in names and definitions. In the case of Burali-FortiТs paradox, the series whose ordinal number causes the difficulty is the series of all ordinal numbers. In each contradiction something is said about all cases of some kind, and from what is said a new case seems to be generated, which both is and is not of the same kind as the cases of which all were concerned in what was said. Let us go through the contradictions one by one and see how this occurs.
AJ.(1) When a man says УI am lying,Ф we may interpret his statement as: УThere is a proposition which I am affirming and which is false.Ф All statement that Уthere isФ so-and-so may be regarded as denying that the opposite is always true; thus УI am lyingФ becomes: УIt is not true of all propositions that either I am not affirming them or they are true;Ф in other words, УIt is not true for all propositions p that if I affirm p, p is true.Ф The paradox result from regarding this statement as affirming a proposition, which must therefore come within the scope of the statement. This, however, makes it evident that the notion of Уall propositionФ is illegitimate; for otherwise, there must be propositions (such as the above) which are about all propositions, and yet cannot, without contradiction, be included among the propositions they are about. Whatever we suppose to be the totality of propositions, statements about the totality generate new propositions which, on pain of contradiction, must lie outside the totality. It is useless to enlarge the totality, for that equally enlarges the scope of statements about the totality. Hence there must be no totality of propositions, and Уall propositionsФ must be a meaningless phrase.
AK.(2) In this case, the class w is defined by reference to Уall classes,Ф and then turns out to be one among classes. If we seek help by deciding that no class is a member of itself, then w becomes the class of all classes, and we have to decide that this is not a member of itself, i.e., is not a class. This is only possible if there is no such thing as the class of all classes in the sense required by the paradox. That there is no such class results from the fact that, if we suppose there is, the supposition immediately gives rise (as in the above contradiction) to new classes lying outside the supposed total of all classes.
AL.(3) This case is exactly analogous to (2), and shows that we can not legitimately speak of Уall relations.Ф
AM.(4) УThe least integer not nameable in fewer than nineteen syllablesФ involves the totality of names, for it is Уthe least integer such that all names either do not apply to it or have more than nineteen syllables.Ф Here we assume, in obtaining the contradiction, that a phrase containing Уall namesФ is itself a name, though it appears from the contradiction that it can not be one of the names which were supposed to be all the names there are. Hence Уall namesФ is an illegitimate notion.
AN.(5) This case, similarly, shows that Уall definitionsФ is an illegitimate notion.
AO.(6) This is solved, like (5), by remarking that Уall definitionsФ is an illegitimate notion. Thus the number E is not defined in a finite number of words, being in fact not defined at all.⁶)
AP.(7) Burali-FortiТs contradiction shows that Фall ordinalsФ is an illegitimate notion; for if not, all ordinals in order of magnitude form a well-ordered series, which must have an ordinal number greater than all ordinals.
AQ.Thus all our contradictions have in common the assumption of a totality such that, if it were legitimate, it would at once be enlarged by new members defined in terms of itself
AR.This leads us to the rule : УWhatever involves all of a collection must not be one of the collection ;Ф or, conversely: УIf, provided a certain collection had a total, it would have members only definable in terms of that total, then the said collection has no total.Ф⁷)
AS.The above principle is, however, purely negative in its scope. It suffices to show that many theories are wrong, but it does not show how the errors are to be rectified. We can not say: УWhen I speak of all propositions, I mean all except those in which Сall propositionsТ are mentioned;Ф for in this explanation we have mentioned the propositions in which all propositions are mentioned, which we can not do significantly. It is impossible to avoid mentioning a thing by mentioning that we wonТt mention it. One might as well, in talking to a man with a long nose, say: УWhen I speak of noses, I except such as are inordinately longФ which would not be a very successful effort to avoid a painful topic. Thus it is necessary, if we are not to sin against the above negative principle, to construct our logic without mentioning such things as Уall propositionsФ or Уall properties,Ф and without even having to say that we are excluding such things. The exclusion must result naturally and inevitably from our positive doctrines, which must make it plain that Уall propositionsФ and Уall propertiesФ are meaningless phrases.
AT.The first difficulty that confronts us is as to the fundamental principles of logic known under the quaint name of Уlaws of thought.Ф УAll propositions are either true or false,Ф for example, has become meaningless. If it were significant, it would be a proposition, and would come under its own scope. Nevertheless, some substitute must be found, or all general accounts of deduction become impossible.
AU.Another more special difficulty is illustrated by the particular case of mathematical induction. We want to be able to say: УIf n is a finite integer, n has all properties possessed by 0 and by the successors of all numbers possessing them.Ф But here Уall propertiesФ must be replaced by some other phrase not open to the same objections. It might be thought that Уall properties possessed by 0 and by the successors of all numbers possessing themФ might be legitimate even if Уall propertiesФ were not. But in fact this is not so. We shall find that phrases of the form Уall properties which etcФ involve all properties of which the УetcФ can be significantly either affirmed or denied, and not only those which in fact have whatever characteristic is in question; for, in the absence of a catalogue of properties having this characteristic, a statement about all those that have the characteristic must be hypothetical, and of the form: УIt is always true that, if a property has the said characteristic, then etc.Ф Thus mathematical induction is prima facie incapable of being significantly enunciated, if Уall propertiesФ is a phrase destitute of meaning. This difficulty, as we shall see later, can be avoided; for the present we must consider the laws of logic, since these are far more fundamental.

¹) Two propositions are called equivalent when both are true or both are false.  back to text1

²) This contradiction was suggested to me by Mr. M.G. Berry  back to text2

³) Cf. König, "Ueber die Grundlagen der Mengenlehre und das Kontinuumproblem," Math. annalen vol. LXI(1905); A.C. Dixon, "On 'well-ordered' aggregates," Proc. London Math. Soc., Series 2, Vol.IV, Part I (1906); and E.W. Hobson, "On the Arithmetic Continuum," ibid. The solution offered in the last of these papers does not seem to me adequate.  back to text3

⁴) Cf. Poincare, "Les mathematiques et la logique," Revue de Metaphysique et le Morale, Mai, 1906, especially sections VII and IX; also Peano, Revista de Mathematica, Vol. VIII, No. 5(1906), pp.149 ff.  back to text4

⁵) "Una questione sui numeri transfiniti," Rendiconti del circolo matematico di Palermo, Vol. XI(1897).  back to text5

⁶) Cf. УLes paradoxes de la logique,Ф by the present author, Revue de Metaphysique et de Morale, Sept., 1906, p. 645.  back to text6

⁷) When I say that a collection has no total, I mean that statements about all its members are nonsense. Furthermore, it will be found that the use of this principle requires the distinction of all and any considered in Section II.   back to text7