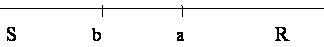Бернард Больцано, ПАРАДОКСЫ БЕСКОНЕЧНОГО

Б. Больцано, Парадоксы бесконечного, параграфы 11-20

§ 11.

Это, столь известное математикам, понятие о бесконечном не удовлетворяет однако некоторых философов, особенно философов новейшего времени, как Гегеля и его последователей. Они называют его презрительно плохим бесконечным и думают, что знают несравненно более высокое, истинное, качественное бесконечное, которое они находят только в Боге и вообще в абсолюте. Если они, как Гегель, Эрдман и другие, представляют себе математическую бесконечность только как величину, которая изменяется и не имеет границ в своем возрастании (что принимается некоторыми математиками, как мы вскоре увидим, за определение этого понятия), – то я охотно присоединяюсь к ним в отрицательном отношении к этому понятию о величине, которая только бесконечно возрастает, но никогда не достигает бесконечности. Действительная бесконечная величина, например, длина целой прямой, неограниченной с обеих сторон (т.е. величина протяжения, заключающего все точки, которые определяются только выражаемым в понятиях отношением к двум данным точкам), не должна быть переменной, чего и нет на самом деле в приведенном здесь примере. Величина, которая может быть всегда взята большей, чем мы ее брали раньше, и которая может стать больше, чем каждая данная (конечная) величина, может при этом оставаться всегда просто конечной величиной, что верно, например, для каждой числовой величины 1, 2, 3, 4, . . . . ²) Я не допускаю только того, чтобы философу известен был какой либо предмет, которому он был-бы вправе приписать свою бесконечность, как качество, не обнаружив раньше в этом предмете, в каком-либо отношении, бесконечной величины или бесконечного количества. Если я могу доказать, что даже говоря о Боге, которого мы рассматриваем как всесовершенно единое, можно указать такие точки зрения, с которых мы видим в нем бесконечное количество, и что эти-то точки зрения и позволяют приписывать ему бесконечность, то вряд-ли нужно доказывать дальше, что подобные соображения лежат также в основе всех остальных случаев, где правильно употребляется понятие о бесконечности. Я же говорю: мы называем Бога бесконечным, потому что мы должны признать, что он владеет силами более, чем одного рода, имеющими бесконечную величину. Так мы должны приписать ему силу познания, которая и есть истинное всеведение, т.е. обнимает бесконечное множество истин, а именно все истины, и т.д. Что же это за понятие об истинно бесконечном, которое нам хотят навязать вместо того, которое мы здесь установили? Это должно быть Все, заключающее в себе каждое нечто, абсолютное Все, вне которого нет ничего. Согласно такому объяснению это была-бы бесконечность, заключающая в себе и по нашему определению бесконечно многое. Это была-бы совокупность не только всех действительных вещей, но также и всего того, что не имеет никакой действительности, совокупность предложений и истин в себе. Итак, не принимая даже в расчет всех остальных ошибок, которые вплетены в это учение о понятии “все”, мы не имеем никакого основания отказываться от нашего понимания бесконечности и принимать учение наших противников.

§ 12.

          Я должен, однако, признать неправильными и отвергнуть также некоторые другие определения бесконечного, которые были предложены даже математиками, полагавшими при том, что эти определения представляют только составные части одного и того же понятия.
          1. В самом деле, как я уже упоминал, некоторые математики, в том числе даже Cauchy (в своем «Cours d’analyse» и некоторых других сочинениях), автор статьи «бесконечное » в словаре Клюгеля (Klugel) считали, что дают определение бесконечного, описывая его, как переменную величину, которая возрастает безгранично и может сделаться больше всякой данной величины, как бы велика она ни была. Граница этого безграничного возрастания должна быть бесконечно большой величиной. Так, тангенс прямого угла, рассматриваемый как величина непрерывная, безграничная, не имеющая конца, является в собственном смысле слова бесконечным. Ошибочность этого определения ясно видна уже из того, что то, что математики называют переменной величиной, на самом деле не есть величина, а только понятие, представление о величине, и при том такое представление, которое заключает в себе не одну величину, а бесконечное множество различающихся по своим значениям величин, то есть величин, которые отличаются друг от друга по своей величине (Grossheit). Называют бесконечным не различные значения приведенного здесь для примера tang. φ при различных значениях φ, а только то единственное значение, о котором думают, хотя в данном случае и неправильно, что это выражение принимает его для значения φ = π/2. Противоречиво также говорить о границе безграничного возрастания и, при определении бесконечно малого, о границе безграничного убывания. Если мы считаем первую определением бесконечно большого, то по аналогии следовало-бы считать нуль (ничто) определением бесконечно малого, что, однако, несомненно неправильно, и чего не позволяют себе говорить ни Cauchy, ни Grunert.
          2. Если вышеприведенное определение слишком широко, то определение принятое Спинозой (Spinoza) и многими другими философами и математиками, напротив того, слишком узко. Это определение состоит в том, что только то бесконечно, что не способно к дальнейшему увеличению, или – к чему не может быть ничто прибавлено (приложено). Математик позволяет себе прибавлять к каждой величине, также и к бесконечно большой, еще другие величины, и не только конечные, но даже и бесконечные; он даже повторяет бесконечную величину бесконечное число раз и т.д. Если некоторые и спорят еще о том, законно-ли это, то какой математик – если только он не отрицает все бесконечное – откажется признать, что длина прямой, ограниченной с одной стороны, но простирающейся в бесконечность с другой, бесконечна, и может быть, несмотря на это, увеличена прибавлениями с первой стороны.
          3. Мы не можем признать более удовлетворительным также определение, предлагаемое теми, которые, придерживаясь точно значения составных частей слова, говорят, что бесконечное есть то, что не имеет конца. Если-бы при этом они имели в виду только конец во времени, т.е. прекращение, то только вещи, существующие во времени, могли-бы называться конечными или бесконечными. Но ведь мы спрашиваем также о вещах, которые существуют не во времени, например, о линиях и вообще о величинах, конечны ли они или бесконечны? Если же понимают это слово в более широком смысле, например, в смысле границы вообще, то я напомню, во-первых, что существуют предметы, для которых нельзя надлежащим образом доказать, что они имеют границу, если не придавать этому слову в высшей степени неопределенного и сбивчивого значения; а между тем никто не причислит их к бесконечным. Так, например, каждая простая часть времени или пространства (точка во времени или пространстве) не имеет границ, а, напротив того, рассматривается сама как граница (промежутка времени или линии), даже определяется многими именно так, как будто-бы это и составляло ее сущность; но, однако, не пришло еще в голову никому (даже Гегелю) увидеть бесконечное в простой точке. Точно также математик не знает границы окружности и столь многих других замкнутых линий и поверхностей, считает их однако предметами конечными (если только он не имеет в виду бесконечного множества точек, заключающихся в них, хотя с этой точки зрения он должен признать нечто бесконечное в каждой ограниченной линии). Я замечу, во-вторых, что существует много предметов, бесспорно ограниченных, но рассматриваемых как величины бесконечные. Это имеет место не только для ранее упомянутой прямой, которая только с одной стороны простирается в бесконечность, но также для площади, ограниченной двумя бесконечными параллельными прямыми или двумя простирающимися в бесконечность сторонами угла, начерченного на плоскости и т.д. Точно также, в рациональной психологии мы назовем бесконечно большой познавательную силу в том случае, когда, не будучи всеобъемлющей, она может обозревать только какое-либо бесконечное множество истин, например, только бесконечный ряд десятичных знаков, заключающихся в единственной величине

.
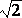
4. Самое обыкновенное определение таково: бесконечно большим называется то, что больше всякой данной величины. Здесь приходится прежде всего определить точнее, что подразумевается под словом «данный». Означает ли оно нечто возможное, т.е. то, что может существовать в действительности или лишь то, что не содержит в себе противоречия? В первом случае понятие конечного ограничивают только разрядом предметов, принадлежащих к реальностям, т.е. таких, которые всегда реальны или были когда то, ли еще только станут реальными, или, по крайней мере, могли-бы когда либо стать реальными. Fries (Naturphilosophie, §47), как кажется, и понимает бесконечность именно в этом смысле, называя ее неосуществимой. В разговорном языке, однако, применяется понятие конечного, также, как и бесконечного, в обоих случаях: и к предметам, которым присуща действительность, как, например, к Богу, и к другим предметам, о существовании которых не может быть и речи, каковы, например, простые предложения и истины сами в себе, вместе со своими составными частями, представлениями в себе; при этом мы допускаем, как конечные, так и бесконечные множества их. Если-же понимать под данным все то, что только не содержит внутреннего противоречия, то уже в самое определение понятия вносится утверждение, что бесконечное не существует, потому что величина, большая, чем каждая величина, не заключающая в себе внутреннего противоречия, должна быть больше самой себя, что, очевидно, нелепо. Но есть еще третье значение, в котором можно принимать слово данный, а именно, если мы под этим словом подразумеваем все, что нам может быть только дано т.е. что может сделаться предметом нашего опыта. Но я обращаюсь с вопросом к каждому, не понимает ли он выражение «конечное» и «бесконечное» именно так (и, если только употребление их должно быть полезно науке, то не должен ли он их понимать непременно в этом смысле), что эти выражения относятся во всяком случае к известным внутренним свойствам предметов, а никоим образом не касаются только отношений их к нашей познавательной способности, даже к нашим чувствам (в том смысле, можем ли мы или не можем производить над ними опытов). Следовательно, вопрос о том, конечно ли что-нибудь или бесконечно, не может зависеть от того, имеет ли предмет, о котором идет речь, такую величину, которую мы можем воспринимать (например, от того, можем ли мы его обозревать или нет).

§ 13.

Как только мы пришли к соглашению, какое понятие мы должны связывать со словом бесконечный, и как только мы уяснили себе вполне составные части этого понятия, то ближайшим вопросом является следующий: обладает ли это понятие предметностью, то есть существуют ли предметы, к которым оно применимо, многообразия, которые мы можем назвать бесконечными в установленном нами значении. На этот вопрос я смело отвечаю утвердительно самым решительным образом. Уже в ряду тех предметов, которые не имеют никаких притязаний на действительность и даже на возможность, бесспорно существуют многообразия бесконечные. Очень легко заметить, что многообразие предложений и истин самих в себе – бесконечно. Если мы станем, например, рассматривать какую-нибудь истину, скажем, что истины вообще существуют, или любую другую истину, которую мы обозначим через A, то мы увидим, что предложение, выраженное словами «A истинно», уже отлично от A, потому что предложение A имеет, очевидно, совершенно другое подлежащее, а именно: подлежащим второго предложения будет все первое предложение A. Далее, по тому самому закону, по которому мы вывели из предложения A отличное от него предложение, которое мы назовем B, мы можем вывести из B третье предложение C, и так далее без конца. Совокупность всех этих предложений, из которых каждое последующее находится к непосредственно предыдущему в только что указанном отношении, а именно, что подлежащим последующего предложения является предыдущее предложение, о котором высказывается, что оно истинно, совокупность эта – утверждаю я – обнимает такое многообразие частей (предложений), которое больше, чем всякое конечное многообразие. Ибо читатель заметит без указаний с моей стороны сходство, которое имеет ряд предложений, составленных по только что приведенному закону образования с рядом чисел, рассмотренных в §8. Сходство это состоит именно в том, что к каждому члену последнего ряда найдется соответствующий в первом ряду, что, следовательно, для каждого числа, как бы велико оно ни было, найдется равное ему число различных предложений, или, лучше сказать, что существуют сами по себе подобные предложения, независимо от того, будем ли мы их составлять или нет. Отсюда следует, что совокупность всех этих предложений имеет множественность, которая больше всякого числа и, следовательно, бесконечна.

§ 14.

          Как ни просто и как ни ясно только что приведенное доказательство, однако есть много ученых и очень остроумных людей, которые считают парадоксальным и даже ложным то предложение, которое я считаю здесь доказанным. Они отрицают существование чего-либо бесконечного. Они утверждают, что не только среди реальных, но и среди остальных предметов нет ни отдельного предмета, ни совокупности нескольких предметов, в которых можно было бы допустить наличность бесконечного множества частей. Мы рассмотрим позже возражения, которые они приводят против бесконечного в области действительного, так как мы только позже приведем основания существования такой бесконечности. Здесь же мы рассмотрим только те положения, которыми пользуются для доказательства того, что нет бесконечного нигде, даже и в области предметов, не имеющих притязаний быть действительными. 1. «Бесконечного множества», как говорят наши противники, «не может быть нигде уже потому, что бесконечное не может быть соединено в одно целое, не может быть объято целиком в “мысли”». Это утверждение я должен назвать попросту ошибочным. Ошибка вытекает из ложного убеждения, что для того, чтобы вообразить себе целое, состоящее из известных предметов a, b, c, d, . . . нужно сперва составить себе представление о каждом отдельном предмете. На самом деле, это совершенно неверно. Я могу вообразить себе множество или совокупность всех жителей Праги или Пекина или, если уж так предпочитают, целое население этих городов, не представляя себе каждого из жителей в отдельности, т.е. не составляя отдельных представлений о каждом. Я это и делаю в данную минуту, говоря об этом множестве и высказывая, например, суждение, что количество это в Праге колеблется между 100000 и 120000. Как только мы имеем представление A, которое соответствует каждому из предметов a, b, c, d, . . . и не соответствует ничему другому, то нам очень легко составить представление о совокупности всех этих предметов. Для этого не нужно ничего другого, как только связать понятие, заключенное в слове совокупность с представлением A таким образом, как это указывают слова: совокупность всех A. Одно это замечание, правильность которого, я думаю, очевидна каждому, уничтожает все трудности, которые хотят усмотреть в понятии о многообразии, состоящем из бесконечного числа частей. Для этого нужно только, чтобы было на лицо родовое понятие, заключающее в себе все эти части [и не] заключающее ничего другого, как это, например, имеет место в понятии «совокупность всех предложений или истин в себе», в котором необходимым родовым понятием является «предложение или истина в себе».
          Я, однако, не могу оставить незатронутой еще другую ошибку, которая таится в обсуждаемом возражении.
          А именно – мнение, которое гласит, что «многообразие не существовало бы, если бы не было кого-либо, кто бы думал о нем». Утверждающий это – если только он желает быть последовательным настолько, насколько это возможно, защищая ошибочное положение – должен не только утверждать, что нет бесконечных многообразий предложений или истин в себе, но должен также утверждать, что нет вообще ни предложений, ни истин в себе. Действительно, если мы уяснили себе вполне понятие о предложениях и истинах в себе и если мы не сомневаемся нисколько в их существовании, то вряд ли мы дойдем до подобных утверждений и уже во всяком случае не будем на них настаивать. Чтобы сделать это вполне очевидным, я позволю себе предложить один вопрос: находятся ли на полюсах земли тела жидкие и твердые, воздух, вода, камни, и т.п., действуют ли эти тела по известным законам друг на друга, например, так, что скорости, которые они передают друг другу при ударе, находятся в отношении обратном к их массам и т.п., и происходит ли это и тогда, когда это не наблюдает ни один человек, ни вообще ни одно мыслящее существо? Если на этот вопрос последует утвердительный ответ (а кто же мог бы ответить иначе?), то имеются предложения и истины в себе, которые выражают все эти явления, несмотря на то, что никто не думает и не знает о них. В этих же предложениях часто говорится о целом, о множестве, потому что каждое тело есть ведь целое и производит многие из своих действий только благодаря множеству своих составных частей. Существуют, следовательно, множества и целые независимо от того, имеется ли существо, которое бы о них думало. А если бы этого не было, если бы даже эти множества не существовали, то каким образом могли бы быть правильными суждения, которые мы о них высказываем? Или, больше того, какой был бы смысл этих суждений, если бы они были истинными лишь постольку, поскольку есть кто-то, воспринимающий эти явления? Когда я говорю «Эта глыба оторвалась на моих глазах от той скалы и упала вниз, рассекая воздух.», то это должно было бы иметь приблизительно следующий смысл: в то время как я представлял себе мысленно известные простые существа там наверху, произошло соединение их, которое я назову глыбой; это соединение отделилось от других соединений, которые, в то время, как я соединял их мысленно, объединились в одно целое, которое я называю скалой и т.д.
          2. Можно было бы, однако, сказать: «при всем том остается все же справедливым тот факт, что исключительно от нас, и по большей части вполне от нашего произвола зависит то, захотим ли мы соединить несколько простых предметов в одну совокупность или нет, и что только в случае, когда мы это делаем, между ними возникают известные отношения. Центральный атом пуговицы на моем сюртуке и центральный атом того яблока на башне не имеют ни малейшего отношения друг к другу и друг с другом ничем не связаны, и только благодаря тому, что я думаю о них одновременно, возникает некоторый род связи между ними.». – Но я должен высказаться и против этого. Еще до того, как мыслящее существо связало оба атома в своем представлении, они уже находились во взаимодействии, например, в силу притяжения и т.п.; и если бы только это мыслящее существо не предприняло под влиянием своих мыслей никаких действий, которые повлияли бы на отношения между обоими атомами, то было бы совершенно неверно утверждать, что только благодаря тому, что их мыслят вместе, между ними возникли отношения, которых без этого не было бы; неправильно также утверждать, что эти отношения не существовали между ними и раньше. Если я сужу правильно, что один атом находится ниже, а другой выше, и что, следовательно, этот притягивается тем несколько вверх и т.д., то все это имеет место и в том случае, когда я не думаю об этом.
          3. Некоторые говорят: «Для того чтобы существовала совокупность, нет надобности в том, чтобы мыслящее существо действительно думало о ней, но необходимо, чтобы о ней можно было думать. А так как мыслящее существо не может представить себе бесконечное множество вещей, каждую в отдельности, и связать затем эти представления в совокупность, то невозможна и совокупность, заключающая в себе бесконечное множество вещей в качестве составных частей».
          Мы уже видели в №1, насколько повторенное здесь предположение, что для того, чтобы помыслить о совокупности, необходимо мыслить все ее части в отдельности, т.е. мыслить каждую отдельную часть при посредстве соответствующего ей единичного представления. Не представляется нам также никакой надобности в том, чтобы указывать на всеведущее существо, как на такое, которого не затрудняет даже понимание бесконечного множества предметов, каждого в отдельности. Мы не должны соглашаться даже и с первым предположением, а именно с тем, что существование совокупности вещей покоится на возможности думать об этой совокупности. Ибо возможность мыслить вещь никоим образом не составляет основания для возможности ее существования. Напротив того, возможность существования вещи составляет основание для того, чтобы разумное существо, если оно только не впадает в ошибку, нашло эту вещь возможной или, как говорят (в переносном смысле), мыслимой, т.е. чтобы ее можно было мыслить. Мы убедимся вполне в правильности этого замечания и в полной несостоятельности, правда, очень распространенного мнения, которое я здесь оспариваю, если постараемся уяснить себе составные части важного понятия “возможности”. Если называют возможным то, что может быть, то это, очевидно, еще не будет разложение понятия о возможности, так как оно заключается целиком в выражении “может быть”. Но еще неправильнее было бы пытаться установить следующее определение: возможно то, что можно мыслить. Мыслить, в собственном значении этого слова, включая сюда уже и простое представление, мы можем и невозможное. Это мы и делаем в действительности каждый раз, когда мы высказываем о нем суждение, – признаем его, например, невозможным. Так, мы говорим, что нет и не может быть величины, которая бы выражалась нулем или

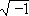
. Но даже если бы мы разумели под мышлением не простое представление, а признание действительного существования, то ложным является утверждение, что возможно все, что мы можем считать истинным. Ведь мы считаем иногда ошибочно и невозможное истинным, как, например, то, что мы нашли квадратуру круга. В таком случае, следовало бы сказать (с поправкой, которую я уже делал выше), что возможно то, о чем мыслящее существо, при условии правильности суждения, высказывает, что оно может случиться, т.е. возможно. Объяснение, заключающее в себе очевидный ложный круг! Итак, мы вынуждены отказаться окончательно от отношения к мыслящему существу при объяснении возможного и поискать другого признака. Иногда говорят, что возможно то, “что себе не противоречит”. Все, что содержит в себе противоречие, конечно, невозможно, так, например, суждение, что шар не есть шар. Но не все невозможное является именно таким, что противоречие содержится уже в составных частях, из которых составлено представление. Невозможно, чтобы тело, ограниченное семью плоскими гранями, имело равные грани, но в данном случае противоречие еще не обнаруживается сразу в соединении слов. Следовательно, мы должны расширить наше определение. Если бы мы сказали, что невозможно все, что противоречит какой-либо истине, то этим мы бы провозгласили невозможность всего, что не существует, потому что суждение, что возможное есть, противоречит истине, что его нет. В таком случае мы не допускали бы никакой разницы между возможным и истинным, и даже необходимым, что мы делаем однако все. Отсюда мы видим, что область истин, которым противоречит невозможное, должна быть ограничена только известным родом их, и вряд ли теперь от нас может ускользнуть, какого рода будут эти истины. Это – истины, содержащие чистые понятия. Что противоречит истине, содержащей чистые понятия, то следует назвать невозможным; возможно, следовательно, то, что не противоречит никакой истине, содержащей чистые понятия. Кто раз постиг, что это и есть правильное определение понятия возможности, тому вряд ли придет на ум утверждать, что нечто возможно лишь тогда, когда оно мыслимо, т.е. когда мыслящее существо не ошибающееся в своем суждении, найдет его возможным. Это ведь значило бы: «Предложение лишь тогда не противоречит истине, содержащей чистые понятия, когда не противоречит никакой истине, содержащей чистые понятия то, что что существует мыслящее существо, которое в согласии с истиной находит, что это предложение не противоречит никакой истине, содержащей чистые понятия». Кто же не заметит, каким лишним, не относящимся к делу является здесь введение этого мыслящего существа? Если же решено, что возможность создается не мышлением, то где же найдется основание для вывода о невозможности бесконечного множества на основании мнимого обстоятельства, что невозможно мыслить совместно бесконечное множество вещей?

§ 15.

          Я считаю теперь достаточно обоснованным и доказанным мнение, что существуют бесконечные множества, по крайней мере, среди вещей нереальных, что именно множество всех истин в себе бесконечно. Подобно тому, как это было сделано в §13, мы придем к заключению, что бесконечно также множество всех чисел (так называемых натуральных или целых чисел, сущность которых мы определили в §8). Но и это положение звучит парадоксально, и мы можем, собственно, считать его первым среди парадоксов, появляющихся в области математики, так как раньше рассмотренный парадокс относится к более общей науке, чем наука о величинах.
          «Если каждое число», можно сказать, «по самому понятию о числе, есть лишь простое конечное множество, то каким образом может быть бесконечным множество всех чисел? Когда мы рассматриваем ряд натуральных чисел

1, 2, 3, 4, 5, 6, . . .
то мы замечаем, что множество чисел, которое содержит этот ряд, начиная с первого (единицы), до какого-нибудь другого, например, до числа 6, выражается всегда этим последним числом. Поэтому множество всех чисел должно быть именно так велико, как последнее из них и, следовательно, само должно быть числом, а не бесконечностью».
          Обманчивость этого вывода исчезает тотчас же, как только мы вспомним, что во множестве всех чисел в натуральном ряду нет последнего числа, что таким образом понятие о последнем (высшем) числе – понятие беспредметное, потому что содержит противоречие. Ибо, по закону образования этого ряда, данном в определении его (§8), каждый член ряда имеет последующий. Одним этим замечанием разрешается уже этот парадокс.

§ 16.

Если множество чисел (и именно так называемых целых чисел) бесконечно, то тем более бесконечно множество величин (по определению, приведенному в §6 и в «Wissenschaftslehre» в §87). В самом деле, по этому определению не только все числа будут величинами, но имеется гораздо больше величин, чем чисел, так как дроби 1/2, 2/3, 1/4, . . . , а равно и так называемые иррациональные выражения

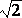
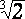
, . . π, e, . . также обозначают величины. По этому определению нет противоречия в том, чтобы говорить о бесконечно больших и бесконечно малых величинах, если под бесконечно большой величиной подразумевается лишь такая величина, которая при раз положенной в основание единице является целым, по отношению к которому, каждое конечное множество этих единиц составляет только часть; а под бесконечно малой величиной подразумевается такая, по отношению к которой сама единица является целым, частью которого будет каждое конечное множество этих величин. Множество всех чисел является неоспоримым примером бесконечно большой величины. Я говорю: величины, а не бесконечно большого числа, потому что, как мы уже заметили в предыдущем параграфе, никак нельзя назвать числом это бесконечно большое множество. Если же величину, бесконечно большую по сравнению с другой величиной, взятой за единицу, мы примем за единицу и станем ею измерять ту величину, которую мы прежде принимали за единицу, то эта последняя представится нам бесконечно малой.

§ 17.

Время и пространство представляют в высшей степени важный род бесконечно больших величин, которые также еще не принадлежат к области реального, хотя и могут определять реальное. Ни время, ни пространство не представляют ничего реального, так как они не представляют из себя ни субстанций, ни свойств субстанций. Они выступают только, как нечто определяющее для всех несовершенных (ограниченных, конечных или, что сводится к одному и тому же, зависимых, сотворенных) субстанций, а именно, каждая из последних должна постоянно пребывать в некотором времени и известном пространстве, таким образом, что каждая простая субстанция в каждом пункте времени, т.е. в каждой простой части времени должна пребывать в какой-нибудь простой части пространства, т.е. в какой-нибудь его точке. Множество простых частей или точек, из которых состоит время и пространство, бесконечно. бесконечно не только количество простых частей, из которых состоит все время и все пространство, т.е. количество точек времени и пространства вообще, но и количество точек времени между двумя точками a и b, как бы близко ни отстояли эти точки друг от друга, тоже бесконечно. Точно так же бесконечно и количество точек пространства между любыми двумя точками пространства a и b, как бы близко не отстояли друг от друга эти две точки. Мне нет нужды защищать эти предложения, так как вряд ли найдется математик, (если только он не отрицает всякой бесконечности), который не согласился бы с ними. Чтобы спасти себя от признания бесконечного, которое здесь столь явно обнаружено, противники всякой бесконечности приводят следующее возражение: «Мы можем, конечно, всегда мыслить большее количество точек времени и пространства, чем то, которое мы мыслили, но количество точек действительно существующих останется всегда конечным». Но на это я возражаю, что ни время, ни пространство, а потому также ни простые части времени, ни простые части пространства не представляют ничего действительного, и что поэтому не сообразно говорить о конечном множестве их, как существующих в действительности. Тем более несообразно воображать, что эти части становятся действительными только через наше мышление. Ибо ведь отсюда следовало бы, что свойства времени и пространства зависят от нашего мышления и нашей оценки истинности, и что, следовательно, отношение диаметра к окружности круга было рационально, пока мы ошибочно считали его рациональным, и что пространство получит только тогда все те свойства, которые мы узнаем впоследствии, когда они нам станут известны. Если же наши противники исправят вышеприведенное выражение в том смысле, что настоящие свойства пространства и времени определяются только мышлением, соответствующим истине, то сказанное ими представит нечто тавтологическое, а именно: истинно то, что истинно; откуда, конечно, нельзя вывести ни малейшего возражения против утверждаемой нами бесконечности времени и пространства. Во всяком случае, нелепо говорить, что время и пространство заключают столько точек, сколько мы их мыслим.

§ 18.

Хотя каждая величина, вообще каждый предмет, который нам представляется бесконечным в каком-либо отношении, должен представляться нам именно в этом отношении, как целое, состоящее из бесконечного множества частей, – невозможно однако утверждать наоборот, чтобы каждая величина, которую мы рассматриваем, как сумму бесконечного множества других конечных величин, была непременно бесконечной. Так, например, всеми признается, что иррациональные величины, как , по отношению к единице, положенной в основание, будут величинами конечными, хотя их можно рассматривать, как составленные из бесконечного множества дробей вида 14/10 +1/100+4/1000+2/10000+. . ., числители и знаменатели которых – целые числа; точно также известно, что сумма бесконечного ряда слагаемых вида a + ae + ae² + ae³ . . in inf. = a/(1 - e), т.е. равняется конечной величине каждый раз, как е<1³). Итак, в утверждении, что сумма бесконечного количества конечных величин сама будет величиной конечной, нет никакого противоречия, потому что иначе оно не могло бы оказаться правильным. Парадокс, который можно было бы в нем усмотреть, происходит только от того, что забывают о том, как складываемые здесь члены становятся все меньше и меньше. Никого ведь не удивит, что сумма слагаемых, в которой каждое последующее слагаемое составляет только половину предыдущего, не может никогда составить больше, чем удвоенное первое слагаемое, потому что в каждом самом далеком члене этого ряда не достает до этого удвоенного числа именно столько, сколько составляет этот последний член.

§ 19.

Мы не могли не заметить уже в примерах бесконечного, приведенных до сих пор, что не следует считать равными между собой все бесконечные многообразия в отношении их множественности. Напротив того, некоторые из них больше, другие меньше, т.е. одно многообразие может заключать в себе другое, как часть (или, наоборот, может само составлять часть другого). Это утверждение также звучит парадоксально для многих. Конечно, всем тем, кто определяет бесконечное, как нечто неспособное к дальнейшему увеличению, должно казаться не только парадоксальным, но даже противоречивым утверждение, что одно бесконечное больше другого. Но мы уже нашли выше, что это мнение опирается на такое понятие о бесконечном, которое не согласно с обыкновенным употреблением этого слова в речи. По нашему определению, соответствующему не только обычному употреблению этого понятия, но и целям науки, никто не может найти ничего противоречивого или даже странного, в мысли, что одно бесконечное множество может быть больше другого. Для кого, например, не будет ясно, что длина прямой,

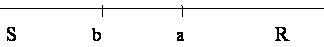
простирающейся безгранично в направлении aR, бесконечна, но что прямая bR, из точки b идущая в том же направлении, больше, чем aR на отрезке ba? и, наконец, что прямая, идущая неограниченно в обоих направлениях aR и aS, должна быть названа большей на величину, которая сама бесконечна, и т.д.

§ 20.

          Перейдем теперь к рассмотрению в высшей степени замечательной особенности, которая может встретиться в отношении двух многообразий, если они оба бесконечны; она, собственно говоря, действительно имеет всегда место, но ее упускали до сих пор из виду в ущерб познанию многих важных истин метафизики, физики и математики – и она, пожалуй, и теперь, когда я это высказываю, покажется в такой степени парадоксальной, что весьма необходимо остановиться несколько дольше на ее рассмотрении. Я утверждаю: два бесконечных многообразия могут быть в таком отношении одно к другому, что, с одной стороны, возможно соединить каждую вещь одного многообразия с некоторой вещью другого в пару таким образом, что не останется в обоих многообразиях ни одной вещи, не соединенной в пару, и ни одна вещь не будет входить в две или несколько пар. С другой стороны, возможно при этом, что одно из этих многообразий заключает в себе другое просто как часть, так что множества, которые они представляют, если рассматривать составляющие их вещи как равные, т.е. как единицы, имеют между собой самые разнообразные отношения. Я докажу это утверждение, приведя два примера, в которых сказанное несомненно имеет место.

          1. Возьмем любые две (отвлеченные) величины, например, 5 и 12; очевидно, что многообразие величин между нулем и пятью (или величин меньших, чем 5), а также многообразие величин, меньших чем 12, бесконечно. Точно также ясно, что последнее многообразие должно считаться большим, чем первое, так как первое составляет только часть второго. Если мы возьмем другие величины вместо величин 5 и 12, то мы принуждены будем сказать, что оба эти многообразия не всегда сохраняют одно и то же отношение друг к другу, а, напротив того, вступают в самые разнообразные отношения. Но не менее всего этого истинно и следующее: если x обозначает любую величину, содержащуюся между 0 и 5, и если мы определим отношение между x и y уравнением

5y = 12x
то y будет величиной лежащей между 0 и 12, и, наоборот, если только y содержится между 0 и 12, то x содержится между 0 и 5. Из этого уравнения следует также, что каждому значению x принадлежит только одно значение y, и наоборот. Отсюда ясно, что для каждой величины многообразия величин между 0 и 5, равной x, существует в многообразии величин, лежащих между 0 и 12, величина, равная y, которая может быть соединена с ней в пару таким образом, что ни одна из вещей, составляющих оба эти многообразия, не останется не соединенной в пару и ни одна не окажется в двух или в нескольких соединениях.

          2. Второй пример заимствуем из пространственной вещи. Кто уже знает, что свойства пространства основываются на свойствах времени, а свойства времени на свойствах отвлеченных чисел и величин, тот не нуждается, конечно, в примере для усмотрения того, что и во времени и в пространстве находятся такие бесконечные многообразия, какие мы нашли в области величин вообще. Однако, ради правильного применения нашего предложения впоследствии, необходимо рассмотреть подробно по крайней мере один случай, в котором бы встречались такие многообразия. Пусть будут поэтому a, b, c три любые точки на прямой; отношение расстояний ab:ac может быть каким угодно, лишь бы ac означало большее из двух расстояний. В таком случае, хотя многообразия точек лежащих на ab и на ac, оба бесконечны,

однако многообразие точек на ac превзойдет многообразие их на ab, так как на ac, кроме точек ab, находятся еще точки bc, которых нет на ab. Если изменить произвольно отношение ab:ac, то мы даже принуждены будем сказать, что и отношение этих многообразий будет совершенно изменено. Относительно этих двух многообразий также справедливо то самое, что прежде было показано для двух многообразий величин, содержащихся между 0 и5 и между 0 и 12, относительно пар, которые можно составить из любой вещи одного многообразия и любой вещи другого. В самом деле, пусть x – точка лежащая на ab; если мы возьмем точку y в направлении ax таким образом, что ab:ac = ax:ay то y будет точкой, лежащей на ac. Если же, наоборот, y – точка, лежащая на ac, если только мы будем определять ax по ay из того же уравнения, то x будет точкой лежащей на ab. Точно также всякое другое x будет определять другое y, и, наоборот, всякое другое y будет определять другое x. Из этих двух истин опять очевидно, что для каждой точки отрезка ab можно выбрать точку отрезка ac и для каждой точки отрезка ac – точку отрезка ab таким образом, что относительно пар, образованных соединением любых двух таких точек, можно утверждать, что нет ни одной точки ни в многообразии точек ab, ни в многообразии точек ac, которая не входила бы в одну из этих пар, и что нет также ни одной точки, которая бы входила в две или более пары.

Примечания
²) Мысль автора заключается, по видимому, в том, что переменная величина, принимающая сколь угодно большие значения, не есть истинно бесконечная величина, потому что каждое значение ее конечно. назад к тексту2

³) Так как обыкновенно доказательство суммирования этого ряда представляется не вполне строгим, то да будет мне позволено по этому случаю привести следующее доказательство. Если мы будем считать а=1 и е положительным (применение этого доказательства к другим случаям делается само собой), и если мы напишем символическое равенство

(1) S = 1 + e + e²+ . . . in inf.

то верно, по крайней мере, то, что S означает величину положительную, конечную или бесконечно большую. Но для каждого целого n

S = 1 + e + e² + . . . + e^{n – 1} + eⁿ + e^{n + 1} + . . . . in inf.

или также

(2) S = (1 – eⁿ)/(1 –e) + eⁿ + e^{n + 1} + . . . . in inf.

вместо чего мы можем также написать

(3) S = (1 – eⁿ)/(1 –e) + P⁽¹⁾,

если обозначим значение бесконечного ряда eⁿ + e^{n + 1} + . . . . in inf. через P⁽¹⁾. При этом мы, по крайней мере, знаем, наверное то, что P⁽¹⁾ означает величину, зависящую от e и от n, измеримую или неизмеримую, во всяком случае положительную. Но тот же бесконечный ряд мы можем представить еще следующим образом:

eⁿ + e^{n + 1} + . . . . in inf. = eⁿ [1 + e + e² + . . . . in inf.]

Здесь сумма бесконечного числа членов, стоящая в скобках в правой части равенства, а именно

[1 + e + e² + . . . . in inf.]

совершенно сходна по виду с рядом, который в символическом равенстве (1) положен = S, но не следует считать ее одной и той же, так как множество слагаемых здесь и в (1), хотя оно и бесконечно в обоих случаях, не будет одним и тем же; здесь в нем несомненно членов на n меньше, чем в (1).
Итак, мы можем с полной уверенностью написать равенство [1+e+e2+ . . . in inf.] = S – P⁽²⁾, при чем мы можем предположить, что P⁽²⁾ обозначает во всяком случае величину, зависящую от n и всегда положительную. Поэтому мы получаем:

(4) S = (1 – eⁿ)/(1 –e) + eⁿ[S – P⁽²⁾] или

S[1 – eⁿ] = (1 – eⁿ)/(1 – e) – eⁿ P⁽²⁾, или, наконец,

(5) S = 1/(1 – e) – {eⁿ/(1 – eⁿ)}P⁽²⁾

Соединение обоих равенств (3) и (5) дает

- eⁿ /(1 – e) + P⁽¹⁾ = { - eⁿ/(1 – eⁿ)}P⁽²⁾

или

P⁽¹⁾ + {eⁿ /(1 – eⁿ)} P⁽²⁾ = eⁿ /(1 – eⁿ),

откуда можно видеть, что если мы примем n сколь угодно большим и сделаем таким образом значение eⁿ /(1 – eⁿ) меньше любой, сколь угодно малой величины 1/N, то каждая из величин P⁽¹⁾ и {eⁿ /(1 – eⁿ)} P⁽²⁾ должна сделаться также меньше любого значения. Но раз это так, то каждое из равенств (3) и (5) показывает, что S = 1/(1 – e), так как S при одном значении e может иметь только одну неизменную величину, следовательно не может зависеть от n. назад к тексту3