Бернард Больцано, ПАРАДОКСЫ БЕСКОНЕЧНОГО

Б. Больцано, Парадоксы бесконечного, параграфы 41-50

§ 41.

          Мы можем теперь, опираясь на данные выше определения и не опасаясь обвинения в противоречии, установить следующие предложения, как бы ни показались парадоксальными некоторые из них для обычного способа представления.
          1. Совокупность всех точек, лежащих между двумя точками а и b, представляет протяжение простого рода или линию, независимо от того, присчитаем ли мы к ней точки а и b (в таком случае, она будет прямой ограниченной), или не присчитаем одной или другой, или обеих крайних точек (в таком случае она будет неограниченной); во всяком случае, она будет всегда той же длины, как и прежде. Каждая подобная неограниченная прямая с той стороны, где недостает крайней точки, именно поэтому не имеет самой крайней (самой отдаленной) точки; за каждой ее точкой находится, напротив того, дальнейшая, хотя расстояние остается всегда конечным.
          2. Периферия треугольника аbc может быть составлена: 1) из прямой аb, ограниченной с обеих сторон, 2) из прямой аc, ограниченной только с одной стороны, при c, и 3) из неограниченной с обеих сторон прямой bc; длина периферии, однако, равна сумме трех длин аb, bc, cа.
          3 Если мы представим себе, что прямая аz разделена пополам в точке b, часть bz разделена опять пополам в точке c, часть cz опять разделена в точке d и что продолжают поступать таким образом без конца; далее, если мы предположим, что эти бесконечно многие точки деления b, c, d,... и точка z мысленно удалены из совокупности точек, лежащих между a и z, то совокупность остальных точек все-таки заслуживает названия линии и величина ее будет та же, что и прежде. Если же мы присчитаем z к совокупности, то нельзя будет уже назвать целое непрерывно-протяженным; в самом деле, точка z является изолированной, ибо для нее нет такого, хотя бы сколь угодно малого расстояния, о котором можно было бы сказать, что на этом расстоянии и на каждом меньшем точка z имеет соседнюю точку в этой совокупности точек. А именно, на всех расстояниях, которые имеют форму   ^az/2ⁿ   не имеется точек, соседних с z.
          4. Если разстояние точек a и b равно разстоянию точек α и β, то и множество точек между a и b должно считаться равным множеству точек между α и β.
          5. Протяжения, которые имеют равное множество точек, имеют также равную величину, но нельзя сказать наоборот, чтобы два протяжения равной величины имели одинаковое количество точек.
          6. В двух протяжениях совершенно подобных между собою, множества их точек должны находиться в таком же отношений, как их величины.
          7. Поэтому, если отношение величин двух совершенно подобных протяжений иррационально, то и отношение множеств их точек будет тоже иррационально. Существуют, следовательно, множества (именно только бесконечные), отношения которых представляют всякого рода иррациональности.

§ 42.

Из этих предложений, число которых (как видим) могло бы быть легко увеличено, насколько я знаю, было обращено внимание в сочинениях математиков только на шестое, и то лишь таким образом, что в противоположность ему было установлено предложение: «подобные линии, как бы ни были они различны по величине, должны иметь одинаковое количество точек». Это утверждал Фишер ¹² в отношении подобных и концентрических дуг, приводя притом, как основание, то, что через каждую точку одной дуги можно провести радиус, который встречает точку другой, Как известно, уже Аристотель занимался этим парадоксом. Заключение Фишера обнаруживает, очевидно, убеждение, что два многообразия, если они даже бесконечны, должны быть между собою равны, как только каждая часть одного может быть соединена в пару с некоторой частью другого. После того, как это заблуждение раскрыто, нет никакой надобности в дальнейшем опровержении этого учения, в котором сверх того вовсе нельзя понять, почему, в случае его правильности, нужно было бы ограничивать утверждение о равном множестве точек только случаем дуг круга, и притом концентрических и подобных: ведь это самое основание могло бы быть приведено также и для всех прямых и для разнообразнейших кривых линий, вовсе не подобных между собою.

§ 43.

Едва ли существует истина в науке о пространстве, против которой учители этой науки так часто грешили, как против той, что «каждое расстояние между двумя точками, а следовательно, и каждая ограниченная с обеих сторон прямая, представляется конечной, т.е. находится с каждой другой в отношении, которое может быть точно определено с помощью понятий. В самом деле, вряд ли найдется геометр, который бы не говорил иногда о бесконечно больших расстояниях и не превращал бы при известных обстоятельствах ограниченной прямой в бесконечно большую. Достаточно указать на известную пару линий, которые, в геометрическом значении этого слова, называют тангенсом и секансом угла или дуги. На основании совершенно ясного определения, они должны представлять пару прямых линий, ограниченных с обеих сторон; однако, как мало найдется людей, которые не решались бы учить, что тангенс и секанс прямого угла бесконечно велики. Это ложное учение немедленно влечет за собою наказание в виде затруднения, возникающего, как только приходится решать, следует ли считать эти две бесконечно большие величины положительными или отрицательными? Действительно, основание, которое можно привести в пользу одного предположения, оказывается справедливым и для другого, так как известно, что прямая, проведенная через центр круга, параллельно к касательной его, имеет совершенно одинаковое отношение к обеим сторонам этой касательной и, следовательно, не встречается с ней ни с одной, ни с другой стороны. В выражении для этих линий 1/0 нет также не малейшего основания к тому, чтобы считать эту предполагаемую бесконечную величину положительной или отрицательной, так как 0 не является ни положительным, ни отрицательным. Поэтому не только парадоксально, но совершенно ложно предполагать существование бесконечно большого тангенса прямого угла, а также всех углов вида:

Напомним при этом случае, что, строго говоря, ни синус, ни тангенс не существуют также и для угла, равного нулю или для угла, равного

nπ. Разница в обоих допущениях только та, что в последнем из них не получается ложного результата, если, в случае, когда эти выражения являются сомножителями, считают произведения несуществующими; в тех же случаях, когда они являются делителями, заключают, что вычисление требует чего-то незаконного.

§ 44.

Таким же незаконным приемом, который, к счастью, нашел мало последователей, является вычисление Iоганна Шульца (loh. Schulz) величины всего бесконечного пространства. Основываясь на том обстоятельстве, что возможно провести прямые линии в бесконечность из каждой данной точки а во все стороны, т.е. во всевозможных направлениях, а также и на том, что каждая мыслимая точка m мирового пространства должна лежать на одной, и только на одной, из этих линий, он счел себя вправе заключить, что можно считать бесконечное пространство шаром, описанным из любой точки а радиусом, равным

; отсюда он тотчас же получил, что все бесконечное пространство имеет величину (4/3)π

³.
Если бы это предложение оказалось правильным, то оно составило бы, конечно, одно из важнейших предложений науки о пространстве. Едва ли можно представить основательные возражения против обеих посылок (которые я излагаю, однако, не точно по Шульцу, так как предо мной нет его книги). В самом деле, если бы кто-нибудь сказал, что вторая посылка ошибочна уже потому, что из нее следует очень неравномерное распределение точек вселенной, а именно более плотное скопление их вокруг произвольно избранного центра а, то этим он показал бы только, что не преодолел еще предубеждения, которое опровергнуто нами в параграфе 21 и след. Ошибка, и совершенно очевидная ошибка, Шульца состоит в том, что прямые, которые должны быть проведены из точки а в беспредельность по всем направлениям, для того, чтобы каждая точка пространства лежала на какой-нибудь из этих линий, он считает однако же радиусами, т.е. линиями, ограниченными с двух сторон. Ведь только из этого выводится шарообразность бесконечного пространства и вычисление его величины = (4/3)π

³. Из этой ошибки вытекает также следующая несообразность: так как для каждого шара существует объемлющий его цилиндр или такой же куб, и еще многие другие протяжения, например, бесконечное количество объемлющих его шаров одного и того же диаметра, то пространство, которое предполагалось целым пространством, оказывается не целым, а только частью, вне которой находится еще бесконечно много других пространств.
Чтобы обнаружить несостоятельность большей части парадоксов (mysteria infiniti), приведенных Босковичем (Воscowich) в Diss. de transformatione locorum geometricorum (прибавление к его Elem. univ. Matheseos Т. III. Romae 1754), достаточно одного замечания, а именно, что прямая, простирающаяся в бесконечность, хотя бы в одну только сторону, по этому самому не может быть линией ограниченной с этой стороны, и что поэтому говорить о ее конечной точке точно также невозможно, как говорить об острии шара или о кривизне прямой, или отдельной точки, или о точке встречи двух параллельных.

§ 45.

          Несколько реже, чем бесконечно большие, вводились также и бесконечно малые расстояния и линии в пространстве, особенно, когда казалось нужным рассматривать, как прямые линии или как плоскости, такие линии и поверхности, которых ни одна часть (имеющая еще протяжение) не является прямой или плоской, например, для более легкого определения их длины или величины их кривизны, или известных замечательных свойств, имеющих значение в механике. В таких случаях позволяли себе даже измышлять расстояния, которые должны быть измеряемы бесконечно малыми величинами второго, третьего и других высших порядков.
          Тот факт, что употребление таких приемов, особенно в геометрии, редко приводило к ложным результатам, произошел благодаря упомянутому в § 37 обстоятельству, а именно благодаря тому, что переменные величины, относящиеся к пространственным протяжениям, поддающимся определению, обладают тем свойством, что, за исключением отдельных изолированных значений, они имеют первую, вторую и каждую следующую производную функцию. В самом деле, где существуют производные, там то, что утверждают о так называемых бесконечно малых линиях, поверхностях и телах, имеет место вообще для всех линий, поверхностей и тел, которые,—хотя и остаются постоянно конечными,—могут быть взяты сколь угодно малыми, т.е, как говорят, могут убывать до бесконечности. Для этих-то переменных и было, собственно, справедливо то, что ложно высказывалось о бесконечно малых расстояниях.
          Само собой понятно, что, при подобном изложении предмета, должны были предлагать и как будто доказывать много парадоксального и даже много совершенно ложного. Каким странным, например, представлялось утверждение, что каждая кривая линия и поверхность есть не что иное, как соединение бесконечно многих прямых линий и плоскостей, которые нужно только предполагать бесконечно малыми; особенно, если наряду с этим признавалось опять существование бесконечно малых линий и поверхностей, которые были однако кривыми. Каким странным является утверждение, что линии, которые в одной из своих точек не имеют кривизны, как например, в точке перегиба, что эти линии имеют в этой точке бесконечно малую кривизну и бесконечно большой радиус. Таким же странным являлось утверждение, что линии, заканчивающиеся в одной из своих точек, имеют в этой точке бесконечно большую кривизну и бесконечно малый радиус кривизны, и тому подобное.

§ 46.

В качестве действительно поразительного и, вместе с тем, очень простого примера того, к каким несообразностям приводит допущение таких бесконечно малых расстояний, я позволю себе привести предложение, которое, по свидетельству Кестнера (Anfangsgrunde der hoh. Analysis, Bd. II, Vorr.), дает уже Галилей в своих «Discorsi e dimostrazioni matematiche etc.», конечно, только с целью вызвать размышление, а именно, что окружность круга так же велика, как его центр.
Чтобы получить представление о том, как пытались это доказать, пусть читатель вообразит себе квадрат abcd, в нем

квадрант bd, описанный из a, как центра, радиусом ab = a; далее, прямую pr, проведенную параллельно ab и пересекающую стороны квадрата ad и bc в p и r, диагональ ac в n, а квадрант в m; словом,— известную фигуру, которая употребляется для доказательства того, что круг радиуса pn равняется кольцу, которое остается после вычитания круга радиуса pm из круга радиуса pr, или, что

¹³)

Если pr подходит все ближе к ab, то очевидно, что круг радиуса pn будет делаться все меньше и меньше, а кольцо между кругами радиусов pm и pr все уже и уже. Геометры, которые не встречали никакого затруднения в том, чтобы допустить бесконечно малые расстояния, распространили это отношение также и на тот случай, когда pr подходит бесконечно близко к ab, так что, например, разстояние ap делается равным dx, и получается уравнение

которое в действительности оказывается просто тождеством. Но в этом случае, согласно их представлению, круг радиуса pn становится бесконечно малым второго порядка; кольцо, которое остается после вычитания круга радиуса pm из круга радиуса pr, получит теперь ширину¹⁴)

mr =

1
–
2

•

dx²
––
a

1
–––
2 • 4

•

dx⁴
––
a³

+ . . .

которая сама представляет бесконечно малую величину второго порядка. Если же принять окончательно, что pr переходить ab, то бесконечно малый круг стягивается в одну точку a, а бесконечно узкое кольцо ширины mr превращается в окружность радиуса ab. Поэтому считали возможным заключить, что простой центр a любого круга радиуса ab имеет одинаковую величину с его окружностью.
Обманчивость этого заключения произошла, главным образом, вследствие введения бесконечно малых. Оно же и приводит читателя к ряду мыслей, которые не дают ему заметить, как много несообразного содержится и в утверждении, что от круга радиуса pn, когда вместо точки p берется окончательно точка a, и когда радиуса pn уже больше не существует, остается еще, однако, центр a, и в утверждении, что кольцо, получаемое от вычитания круга с меньшим радиусом pm из круга с большим радиусом pr, когда оба радиуса, а следовательно, и оба круга, сделаются равными друг другу, обращается в окружность того круга, который был раньше большим. В самом деле, в случае бесконечно малых величин, конечно, привыкли считать те же самые величины то равными между собою, то одну больше или меньше другой на бесконечно малую величину высшего порядка, то совершенно равными нулю. Если мы будем выводить правильные заключения, то из правильно составленного уравнения

в котором сравниваются только величины (площадей) кругов, о которых идет речь, мы можем заключить только, что в случае, когда pr и pm станут равными между собою, круг радиуса pn не будет иметь никакой величины и потому не будет вовсе существовать.
Конечно, справедливо (и я сам установил посылки, ведущие к этой истине, в § 41), что существуют круги с периферией и без нее, и что это не изменяет их величины, которая зависит только от величины их радиуса. Кто-нибудь мог бы вывести отсюда еще новое мнимое доказательство предложения Галилея, исходя из требования, допустимого во всяком случае, чтобы воображать себе круг радиуса pm без периферии, а круг радиуса pr с периферией. Тогда, после отнятия круга радиуса pm от круга радиуса pr и перехода от pr к ab, в действительности останется только окружность круга радиуса ab. Однако, и теперь все-таки невозможно говорить о круге около a, который стягивается в одну точку, и еще менее будет возможно ссылаться на вышеприведенное уравнение с целью вывести из него следствие, что точка a и известная окружность будут равны между собою, так как сказанное уравнение имеет в виду только величины трех кругов, взятых с перифериями или без них.

§ 47.

          Сам изобретатель этого примера, как уже было упомянуто выше, предложил его не с тою целью, чтобы ему удивлялись,, как научной истине. Однако, как серьезную истину, излагают следующее предложение об обыкновенной циклоиде. Циклоида имеет бесконечно большую кривизну в точке ее встречи с основанием, или (что представляет то же самое) она в этой точке имеет бесконечно малый радиус кривизны и перпендикулярна в ней к основанию. Это утверждение совершенно справедливо, если понимать его так, что радиус кривизны бесконечно уменьшается, когда дуга циклоиды бесконечно приближается к основанию; а также, что направление ее в этой точке перпендикулярно к основанию. Но то, что говорится о радиусе кривизны бесконечно малом или (выражаясь правильнее) обращающемся в нуль, сводится лишь к следующему. Кривая, как известно, простирается бесконечно в обе стороны над основанием и, следовательно, не имеет концов; поэтому в рассматриваемой точке сходятся также две дуги и притом так, что будучи перпендикулярны к основанию, они образуют здесь острие, а именно такое острие, в котором обе имеют одно и то же направление или (по менее правильному выражению) направления их образуют угол равный нулю.
          Однако, можно убедиться с помощью вычислений, что все это так и есть на самом деле, и все-таки не понимать, как это происходит или даже, как это возможно. Чтобы сделать и это очевидным, а это необходимо для разрешения парадокса, мы должны сперва понять, почему направление, в котором поднимается обыкновенная циклоида над своим основанием, является перпендикулярным.
          Из самого способа построения обыкновенной циклоиды (через каждую точку O основания проводят дугу круга, который, касаясь основания, имеет радиус, равный радиусу образующего круга, и, отсекая от дуги часть Om, равную по длине разстоянию точки O от начальной точки a, рассматривают m, как точку циклоиды) обнаруживается тотчас же, что угол maO тем ближе подходит к прямому, чем ближе точка O подходит к a, так как угол mOa, который измеряется половиной дуги om, делается

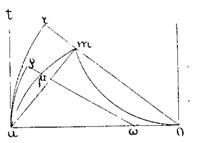все меньше и меньше, а отношение обеих сторон Oa и Om в треугольнике mOa все более и более приближается к отношению равенства; поэтому и углы при третьей стороне am отличаются все меньше и меньше от прямого. Действительно, вычисление показывает это совершенно ясно. Отсюда сверх того следует, что дуга циклоиды am лежит всеми своими точками по одну сторону хорды am, а именно между нею и восстановленным в точке a перпендикуляром at и, следовательно, этот перпендикуляр определяет направление кривой в точке a. Далее, если мы из точки O, как центра, опишем радиусом Oa дугу, выходящую из точки a, то она, очевидно, пересечет хорду Om только в точке ее продолжения r, так как должно быть Or = Oa > Om. Если μ есть какая-нибудь точка кривой, лежащая еще ближе к a, то существует для нее другая точка ω, лежащая на aO еще ближе к a и имеющая то свойство, что для хорды ωμ будет справедливо то же самое, что только что было сказано об Om, а именно, что дуга, описанная из a, как центра, радиусом ωa, встречает продолжение ωμ в сторону точки μ в некоторой точке ρ. Но, вследствие того, что ωa < Oa, дуга aρ лежит внутри дуги окружности ar, т.е. между дугой циклоиды aμ и дугой окружности ar. Мы видим поэтому, что для каждой дуги окружности ar (каким бы малым радиусом Oa она ни была описана), которая касается циклоиды am в a, существует другая дуга aρ, которая в этой области подходит к циклоиде еще ближе. Другими словами, не существует столь малого круга, который можно было бы рассматривать, как меру кривизны в a, если здесь кривизна существует. Поэтому здесь в действительности нет никакой кривизны, и кривая, которая не оканчивается в этой точке, имеет здесь, как мы уже знаем, острие.

§ 48.

          Часто находили парадоксальным также и то, что некоторые пространственные протяжения, простираясь в бесконечном пространстве (т.е. имея точки, разстояние которых друг от друга превосходит всякое данное расстояние), тем не менее, имеют величину конечную; другие же, которые ограничены конечным пространством (т.е. все точки которых лежат так, что их разстояния друг от друга не превосходят некоторого данного расстояния), имеют бесконечно большую величину; или, наконец, что, некоторые пространственные протяжения сохраняют конечную величину, хотя и делают бесконечно много оборотов вокруг одной точки.
          1. Мы должны здесь прежде всего различать, следует ли понимать под пространственным протяжением, о котором будет речь, целое, состоящее из нескольких, отделенных друг от друга, частей (например, гипербола о четырех ветвях), —или вполне односвязное целое, т.е. протяжение, не имеющее ни одной протяженной части, в которой не было бы, по крайней мере, одной точки такого свойства, что, если ее присчитать к остальным частям, то она составит с ними опять одно протяжение.
          Что протяжение, состоящее из отделенных друга от друга частей, может простираться в бесконечное пространство, не делаясь само вследствие этого бесконечным,— этого не найдет странным никто, кто только подумает, что и бесконечный ряд величин, убывающих в геометрической прогрессии, представляет только конечную сумму. В этом смысла может, конечно, и линия простираться в бесконечность, оставаясь при этом конечной, как например, та, которая получится, если мы из данной точки a в данном направлении aR отложим ограниченную прямую ab, затем отложим в некотором разстоянии, остающемся все время неизменным, прямую cd, которая вдвое меньше предыдущей, и будем поступать по тому же закону, продолжая этот процесс бесконечно.
          Если же мы говорим (что и будем делать впредь постоянно) только о таких пространственных протяжениях, которые представляют односвязное целое, то ясно, конечно, что нельзя найти среди протяжений наинизшего порядка, т.е. среди линий, ни одной, которая бы простиралась в бесконечность и сама не имела бы бесконечной величины (длины). В самом деле, это представляет необходимое следствие известной истины, что только прямая линия есть кратчайшая вполне односвязная линия, соединяющая две данные точки¹⁵).
          Иное мы видим в случае поверхностей, которые, при той же длине, можно уменьшить сколь угодно, уменьшая ширину, а также и в случае тел, которые, при той же длине и ширине, могут быть сколь угодно уменьшены путем уменьшения их высоты. Отсюда понятно, почему поверхности, при бесконечной длине, и тела, при бесконечной длине и ширине, сохраняют иногда конечную величину. Мы представим пример, понятный даже для самого несведущего. Представим себе, что на бесконечно простирающейся прямой aR отложены равные отрезки ab = 1 = bc = cd и т.д. до бесконечности; далее, над первым отрезком ab вообразим

квадрат ba, над вторым bc—прямоугольник cγ, который имеет только половину высоты bc, и так над каждым следующим отрезком — прямоугольник, который вдвое ниже, чем предыдущий. Тогда легко убедиться, что связная площадь, представляющаяся здесь, простирается в бесконечность и, однако, будет не больше, чем 2. Не более трудно будет представить себе куб, сторона которого = 1, и приставить мысленно к нему снизу второе тело, основание которого представляет квадрат со стороною 2, т.е. в 4 раза больший, чем основание предыдущего куба, высота же составляет только 1/8; к этому приставить снизу третье тело, основание которого вчетверо больше основания предыдущего, высота же составляет только 1/8 высоты предыдущего; представим себе продолжение этого процесса по тому же закону до бесконечности. Тогда будет понятно, что длина и ширина подставляемых здесь тел увеличивается до бесконечности, хотя их объем делается все меньше и меньше, а именно, каждое последующее тело составляет только половину предыдущего, так что величина пирамидального целого, которое получается таким образом, несмотря на бесконечное основание, не превзойдет никогда объема, равного 2.
          2. Вышерассмотренный случай, в котором протяжение, имеющее в себе нечто бесконечное (бесконечную длину или ширину), оказывается имеющим, однако, величину конечную, может встретиться только в двух высших родах протяжения, в поверхностях и телах, а не в линиях. Теперь же мы будем говорить о случае противоположном, когда протяжение, кажущееся конечным, потому что ограничено конечным пространством, на самом деле имеет, однако, величину бесконечную. Этот случай может иметь место только в двух низших родах протяжения, в линиях и поверхностях, но — никогда не в телах. Тело, не имеющее таких точек, взаимные разстояния которых превосходили бы любую данную величину, наверно не может быть никогда бесконечно большим. Это вытекает непосредственно из известной истины, что из всех тел, в которых взаимные разстояния точек не превышают данного расстояния ε, наибольшим будет шар диаметра ε. В самом деле, шар, описанный из одной из этих точек радиусом ε, заключает все эти точки, а величина шара равна только (π/6)•ε³; поэтому каждое другое тело, не превосходящее этого пространства, будет необходимо меньше, чем (π/6)•ε³. Линий же, которые можно начертить на протяжении хотя бы самой малой поверхности, например, квадратного фута, существует бесконечное множество, и возможно дать каждой из них конечную величину, например, длину квадратного фута, а прибавлением одной или даже бесконечно многих соединительных линий можно образовать из них всех одну связную линию, длина которой в таком случае будет несомненно бесконечной. Совершенно так же существует бесконечное количество поверхностей, которые можно вписать в пространство сколь угодно малого тела, например, кубического фута, и каждой из них мы можем дать величину, например, квадратного фута; а прибавив одну или бесконечное количество соединительных поверхностей, мы можем соединить их все в одну, величина которой, бесспорно, будет бесконечно большой. Все это не должно удивлять никого, кто только не забывает, что линии, плоскости и тела измеряются не одной и той же единицей меры, и что, хотя множество точек в каждой сколь угодно малой лиши бесконечно, нужно, однако, допустить, что в каждой сколь угодно малой, поверхности это множество, во всяком случае, в бесконечное число раз больше, чем в линии, и также, наконец, несомненно, что в теле оно в бесконечное число раз больше, чем в поверхности.
          3. В третьем парадоксе, о котором мы упомянули в начале этого параграфа, говорится, что существуют протяжения, которые делают бесконечное число оборотов вокруг одной точки и сохраняют все-таки при этом величину конечную. Если это протяжение должно быть линейным, то, как мы видели только что в No1, это может иметь место только в том случае, когда вся линия находится в конечном пространстве. При этом же условии нет ничего непонятного в том, что она сохраняет конечную длину, хотя и делает бесконечно много оборотов вокруг данной точки. Для этого должно быть только соблюдено еще дальнейшее условие, что эти обороты, начиная с некоторой конечной величины, бесконечно убывают надлежащим образом. Требование же это может быть выполнено, благодаря тому обстоятельству, что обороты будут происходить вокруг одной только точки. В самом деле, благодаря этому оказывается возможным, чтобы разстояние отдельных точек одного оборота от центра, а следовательно, также и их расстояния между собой, убывали бесконечно, при чем, как это видно уже для окружности, и длина этого оборота может быть бесконечно уменьшена. Логарифмическая спираль сама собой наверно представится нашему читателю, как пример линии, о которой мы здесь говорили; следует принять во внимание только ту ее часть, которая, начиная с некоторой данной точки, постоянно приближается к центру, никогда однако его не достигая.
          Если же пространственное протяжение, делающее бесконечно много оборотов вокруг одной данной точки, должно быть поверхностью или телом, то не представляется надобности даже и в ограничительном условии, чтобы ни одна из точек протяжения не удалялась от центра дальше определенного расстояния. В самом деле, для того чтобы возможно скорее понять мою мысль, пусть читатель представит себе упомянутую спираль, как некоторый род линии абсцисс, из каждой точки которой проводятся ординаты перпендикулярно к ней и ее плоскости. Совокупность всех этих ординат образует тогда, очевидно, поверхность (из рода цилиндрических), которая, с одной стороны, приближается в бесконечном количестве оборотов к центру, никогда не достигая его; с другой же стороны — удаляется в бесконечность. Величина этой поверхности будет зависеть от закона, по которому мы будем увеличивать или уменьшать ординаты. Часть, приближающаяся к центру, останется всегда конечной, если только ординаты этой стороны (т.е. только ординаты, отвечающие конечной ветви линии абсцисс) не будут увеличиваться до бесконечности, потому что каждая поверхность, которой абсциссы и ординаты не возрастают до бесконечности, будет конечной. Но и та часть поверхности, которая находится над другой ветвью спирали, удаляющейся в бесконечность, останется конечной, если только ординаты убывают в более быстром отношении, чем возрастают абсциссы (т, е. длины дуг спирали). Поэтому, если. мы примем за линию абсцисс натуральную спираль, в которой ветвь, приближающаяся к центру (считая от точки, в которой радиус = 1), имеет длину ||/ 2 , и если для ограничения поверхности возьмем дугу гиперболы высшего порядка, имеющей уравнение ух² = a³, то та часть этой поверхности, которая отвечаег x = а и всем большим значениям x, будет иметь только величину а², между тем как другая, отвечающая всем меньшим значениям x, будет увеличиваться до бесконечности. Если же мы возьмем a > ||/ 2 , и переставим конечную точку абсциссы x = a в ту точку спирали, которая имеет радиусом 1, то центр совпадает с конечной точкой абсциссы x = a — ||/ 2 , и потому будет иметь конечную ординату,¹⁶) а часть поверхности, отвечающая этой ветви спирали, будет не больше, чем

a³(

1
––
a

–

1
––
x

) = a² –

a³
––––––
a – ||/ 2

= – (

a³
––––––
a – ||/ 2

– a²);

вся же поверхность, покрывающая спираль по обе стороны (чтобы получить величину этой поверхности, мы должны сложить величины обеих ее частей, беря их положительный значения), будет поэтому =

= a² + (

a³
––––––
a – ||/ 2

– a²) =

a³
––––––
a – ||/ 2

Таким образом, например, для a = 2 вся поверхность выражается только числом 4(2 + ||/ 2 ).
Подобные обстоятельства имеют место также для телесных протяжений. Следует только заметить, что здесь часть тела, стремящаяся к центру, стала бы входить в пространство своих собственных оборотов, если бы мы стали увеличивать ее протяжение в ширину и толщину. Если желательно избежать этого и иметь тело, все части которого лежать каждая вне другой, то можно достигнуть этой цели, например так: возьмем поверхность такого рода, как рассмотренная нами выше, которая, при приближении к центру, все увеличивается в ширину, и придадим ей еще третье измерение,—толщину, которая, однако, при приближены к центру, уменьшалась бы в таком отношении, чтобы составлять постоянно менее половины расстояния между двумя ближайшими оборотами спирали.

§ 49.

          Пространственные протяжения, имеющие бесконечную величину, находятся к этой самой величине в столь разнообразных и часто столь парадоксальных отношениях, что мы должны рассмотреть в отдельности, по крайней мере, некоторые из этих отношений.
          Что протяжение, заключающее в себе бесконечное множество точек, вследствие этого еще не должно быть непрерывным протяжением, и что в непрерывном протяжении величина его вовсе не определяет множества его точек; что из двух протяжений, которые мы считаем равновеликими, одно может заключать на бесконечное множество точек больше или меньше, чем другое; далее, что поверхность может даже заключать в себе в бесконечное число раз больше или меньше линий, тело в бесконечное число раз больше или меньше поверхностей, чем протяжение того же рода, которое мы считаем с ним равновеликим—все это мы в праве считать достаточно разъясненным выше.
          1. Первое, на что мы хотим обратить внимание читателя, это то, что множество точек, которое заключает в себе хотя бы самая короткая прямая az, должно быть рассматриваемо, как множество, которое в безконечно большое число раз больше бесконечного же множества, получаемого из первого следующим образом: начиная с одного из концов, с точки a, берем в надлежащем расстоянии вторую точку b, за нею, в меньшем расстоянии, третью точку c, и так продолжаем без конца, уменьшая эти расстояния по такому закону, чтобы бесконечное их множество в сумме было равно или меньше расстояния az. В самом деле, так как бесконечно многие части ab, bc, cd . . . на которые распадается az, все суть линии конечные, то с каждой из них можно поступить точно так же, как мы только что поступили с az, т.е., в каждой можно будет опять указать такое же бесконечное множество точек, как и в az, и эти точки будут находиться также в az. Следовательно, в целой линии bz такое бесконечное множество точек должно заключаться бесконечное число раз.
          2. Каждой прямой или даже вообще пространственному протяжению, которое (геометрически) равно другому (т.е. совпадает с ним во всех признаках, которые, с помощью сравнения с данным расстоянием, можно выразить в понятиях), должно приписать одинаковое множество точек, если мы в них одинаково выберем границы, например, в линиях, присчитаем концы или не присчитаем их. В самом деле, противное могло бы иметь место только в том случае, если бы существовали расстояния, которые, будучи равными, допускали бы неодинаковое множество точек между теми точками, между которыми они служат расстояниями. Однако, это противоречит понятию, которое мы связываем со словом «геометрически равный», потому что мы называем расстояние ac только тогда

неравным расстоянию ab, а именно большим, когда точки b и c лежат по одну сторону точки a, и точка b находится между a и c, так что все точки, лежащие между a и b будут лежать также между a и c но не наоборот, т е. не все точки, лежащие между a и c, будут лежать также и между a и b.
          3. Если мы обозначим множество точек, лежащих между a и b, вместе с a и b, через E, и примем прямую ab за единицу всех длин, то множество точек прямой ac, которая имеет длину n (под n мы разумеем теперь только целое число), если присчитать и ее крайние точки a и c, будет равно nE—(n — 1).
          4. Множество точек, содержащихся в площади квадрата, сторона которого равна 1 (в обыкновенной мере площадей), будет равно E², если мы присчитаем и периферию ее.
          5. Множество точек в каждом прямоугольнике, одна сторона которого имеет длину m, другая—длину n, будет равно mnE² – [n(m – 1) + m (n – 1)] E + (m – 1) (n – 1), если присчитать и периферию его.
          6. Множество точек в кубе, сторона которого = 1 (в обыкновенной мере тел), будет E³, если мы присчитаем и точки его поверхности.
          7. Множество точек в параллелепипеде, стороны которого имеют длины m, n, r, с присоединением поверхности, будет равно

mnr•E³ – [nr(m – 1) + mr(n – 1) + mn(r – 1)]E² +

+ [m(n – 1) (r – 1) + n(m – 1)(r – 1) + r(m – 1)(n – 1)]E – (m – 1)(n – 1)(r – 1).

8. Прямой, простирающейся бесконечно в обе стороны, мы должны приписать бесконечную длину и множество точек, которое будет в бесконечное число раз больше, чем множество точек прямой, принятой за единицу и равной E. Мы должны признать также, что все такие прямые имеют равную длину и равное множество точек, так как определяющие их части, с помощью которых могут быть определены для двух таких прямых две точки, через которые они проходят (если мы возьмем одинаковое разстояние между этими точками), будут не только подобны друг другу, но и (геометрически) равны.
9. Положение любой точки на такой прямой совершенно одинаково с обеих сторон прямой и представляет лишь такие признаки, допускающие выражение в понятиях, какие представляет положение каждой другой точки. Тем не менее, нельзя сказать, что такая точка разделяет линию на две части одинаковой длины, потому что, если бы могли сказать это об одной точке a, то, на том же основании, мы бы должны были утверждать это о каждой другой точке b, что однако заключает в себе противоречие, так как если бы длина aR была равна длине aS, то не могло бы быть bR(= ba + aR) = bS(= aS — ab).

Напротив того, мы должны утверждать, что прямая, простирающаяся неограниченно в обе стороны, совсем не имеет середины, т.е. не имеет такой точки, которая могла бы быть определена только с помощью выражаемого в понятиях отношения ее к этой линии.
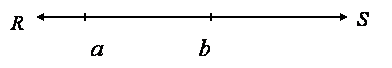
          10. Плоской поверхности, которую заключают между собою две параллельные прямые, неограниченные с обеих сторон (т.е. совокупности всех тех точек, которые содержат перпендикуляры, опущенные из каждой точки одной из этих параллельных прямых на другую), мы должны приписать бесконечно большую площадь и множество точек, которое в бесконечное число раз больше множества точек в квадрате, равном E² и принятом за единицу площадей. Всем подобным полосам, ограниченным параллельными прямыми, если они имеют одинаковую ширину (длина перпендикуляра), мы должны приписать равную величину и равное множество точек. В самом деле, их также можно определить таким образом, что определяющие части не только подобны, но и равны геометрически между собой, например, если мы определяем их с помощью равносторонних прямоугольных треугольников с равными сторонами, при чем будет установлено, что одна из параллельных проходит через основание, а другая через вершину треугольника.
          11. Положение любого перпендикуляра в такой полосе, ограниченной параллельными прямыми, одинаково с обеих сторон плоскости и не представляет никаких других, выражаемых в понятиях, признаков, по сравнению с положением каждого другого перпендикуляра. Несмотря на это, невозможно сказать, что такой перпендикуляр делит плоскость на две геометрически равные друг другу части, потому что такое предположение привело бы нас, как в №9, к противоречию, чем и доказывается его неправильность.
          12. Если мы возьмем плоскость, простирающуюся во всех направлениях в бесконечность, то мы должны приписать ей бесконечно большую площадь и множество точек, которое в бесконечное число раз больше множества точек, заключающихся в полосе, ограниченной параллельными прямыми. Совершенно так, как подобным полосам одинаковой ширины, мы должны также приписать и безграничным плоскостям равное бесконечное множество точек. В самом деле, для них оказывается также верным то, что они могут быть определены не только при помощи подобия, но и (геометрического) равенства: например, если мы будем определять каждую из них с помощью трех точек, лежащих на ней и образующих подобные и равные треугольники.

13. Положение неограниченной прямой, взятой произвольно на такой безграничной плоскости, совершенно одинаково на обеих сторонах плоскости; оно представляет, кроме того, те же самые, выражаемые в понятиях, признаки, как и положение всякой другой прямой этого рода. Однако, невозможно сказать, что такая прямая разделяет плоскость на две геометрически равные части, потому что, если бы стали утверждать это о прямой RS, то должны были допустить это и в отношении всякой другой R'S', что ведет, однако, к явному противоречию, как только мы возьмем эти прямые параллельными между собой.

14. Две неограниченные прямые, которые, находясь в одной плоскости, не параллельны между собою и, следовательно, где-нибудь пересекаются и образуют четыре угла (noпарно равных), делят все пространство неограниченной плоскости на четыре части, из которых каждые две, заключающиеся в равных (подобных) углах RaS = R’aS’ RaS’ = R’aS, подобны между собою. Каждое из этих четырех пространств, заключающихся в углах, содержит в себе бесконечное множество, простирающихся с одной стороны в бесконечность, полос любой ширины, ограниченных параллельными прямыми и подобных тем, о которых мы говорили в №11. Если мы мысленно отбросим любое конечное множество полос, то останется еще угловое пространство, заключающееся в

угле, равном первоначальному. Но совершенно так же, как после объяснений, изложенных в №9 и №11, мы не в праве назвать равными стороны этих углов или полосы, которые являются частями занимаемого ими пространства,—точно так же, и на подобных же основаниях, мы не в праве назвать равными по величине и эти бесконечные угловые пространства, заключенные хотя бы и в равных углах. Так, относительно двух частей плоскости, ограниченных углами RaS и PαΣ, мы видим ясно, что первая больше второй, хотя углы и равны друг другу, если bΣ||aS, cP||aR.
          15. Пространство, которое заключают между собою две параллельные безграничные плоскости (т.е. совокупность всех тех точек, которые находятся на всех перпендикулярах, опущенных из каждой точки одной плоскости на другую), этот (если его так можно назвать) безграничный телесный слой, мы должны считать, во всяком случае, бесконечно большим, какова бы ни была его ширина (т.е. длина такого перпендикуляра). При равной ширине двух таких телесных слоев мы можем назвать равными эти величины, а также можем считать равными множество точек в двух таких телесных слоях, основываясь на том же заключении, которым мы пользовались уже много раз (№№8, 10, 12).
          16. Положение, которое занимает в безграничном телесном слое произвольно взятая, перпендикулярная к его плоскостям и ограниченная параллельными прямыми полоса, является совершенно сходным с обеих сторон телесного слоя, и положение всякой другой полосы этого рода в отношении к этому самому безграничному телесному слою, или к любому другому, является также подобным. Однако, нельзя сказать, чтобы обе части телесного слоя, отделенные одна от другой полосою, должны были иметь непременно равные величины.
          17. Две неограниченные пересекающиеся плоскости разделяют все неограниченное пространство на четыре большие части, из которых каждые две противолежащие бесспорно подобны одна другой, но не должны еще считаться вследствие этого равными.
          18 Так же мало следует считать равными по величине два телесных пространства, которые заключаются между продолженными в бесконечность гранями двух подобных или (как говорят) равных телесных углов.
          19. Точно так же не следует считать геометрически равными, т.е. имеющими равную величину, а тем более заключающими одинаковое множество точек, те две части, на которые делит пространство бесконечная плоскость, хотя они и будут бесспорно подобными.

§ 50.

          Остается еще рассмотреть кратко те парадоксы, которые мы встречаем в области метафизики и физики.
          В этих науках я устанавливаю следующие предложения: «во вселенной нет двух совершенно равных вещей а, следовательно, и двух совершенно равных атомов или простых субстанций, но необходимо допустить существование подобных простых субстанций, как скоро допускается существование сложных тел в мире; наконец, необходимо также предположить, что все эти субстанции переменны и постоянно изменяются». Я утверждаю все это, потому что мне кажется, что это все суть истины, которые могут быть так же строго и ясно доказаны, как любое предложение в математике. Несмотря на это, я должен опасаться, что большая часть физиков отнесется неодобрительно к этим предложениям. Они ведь ставят себе в заслугу установление только таких истин, которым их учить опыт, а опыт не обнаруживает никакой разницы между мельчайшими частицами тела, в особенности одного рода, например, между мельчайшими частицами золота, добытого из того или другого рудника. Далее, говорят они, опыт учит, конечно, что каждое тело сложно, но никто не видел атомов, так как они, будучи совершенно простыми, не имеют никакого протяжения. Опыт показывает, наконец, что различные вещества, например, кислород, водород и т.д. входят между собою то в одни, то в другие соединения и оказывают то одно, то другое действие, – но чтобы они сами претерпевали вследствие этого внутренние изменения, чтобы, например, кислород превратился постепенно в другое вещество, – это, по их мнению, простая выдумка.
          1. По моему мнению, ошибочно утверждать, что опыт учить нас вышеприведенным положениям. Опыт, простой, непосредственный опыт или восприятие, не соединенное с известными истинами, касающимися чистых понятий, учит нас только тому, что мы вообще имеем те или другие восприятия или представления. Откуда являются эти представления, вследствие ли действия какого-либо отличного от нас предмета, нуждаются ли они вообще в какой-нибудь причине, и какие свойства имеет эта причина, – в этом отношении непосредственное восприятие не учит нас ровно ничему; об этом мы выводим заключения только на основании истин, касающихся чистых понятий и придумываемых нашим разумом; заключаем мы, в большинстве случаев, по простому правилу вероятности, о том, например, что красный цвет, который мы теперь видим, вызван болезненным состоянием наших глаз, а ощущение запаха вызвано близостью цветка Напротив, для того, чтобы заметить, что между любыми двумя вещами должно быть какое-нибудь различие, нет надобности ни в каком выведенном из опыта заключении простой вероятности. Напротив того, мы можем прийти к этому с полной достоверностью после небольшого размышления. Если A и B – две вещи, то именно вследствие этого должна иметь место истина, что вещь A не есть вещь B, – истина, которая предполагает существование двух представлений A и B, из которых одно служит представлением только вещи A, но не B; другое же только вещи B, но не A. В этом уже обстоятельстве лежит, конечно, различие (и притом внутреннее) между вещами A и B. Если мы видим таким образом, что между любыми двумя вещами необходимо есть известные различия, то каким образом можем мы себе позволить сомневаться в таком различии только потому, что мы его иногда не замечаем. Для того, чтобы его заметить, ведь нужна особая острота чувств и много других обстоятельств.
          2. Правильно то, что только опыт учит нас тому, что существует много вещей, оказывающих на нас свое действие, и что именно те, которыми обуславливаются наши восприятия, сложны. Однако, опыт учит нас этому только в предположении известных истин, касающихся чистых понятий, как например, той, что различные действия вызываются различными причинами, и т.д. Но не менее верны и выражающиеся в понятиях истины, что каждая причина должна быть чем-то действительным, что все действительное есть или субстанция, или совокупность многих субстанций либо свойств одной либо многих субстанций; равным образом, что свойства, представляющие нечто действительное, не могут существовать без существования субстанции, в которой они находятся, а совокупности субстанций не могут существовать без субстанций, которые составляют части этих совокупностей. Однако, отсюда следует со строгой необходимостью существование простых субстанций, и было бы смешным не признавать их существования только потому, что мы их не видим; и это делается еще более несообразным, когда дальнейшее размышление учит, что каждое тело, которое мы можем воспринимать с помощью внешних чувств, должно быть сложно, даже должно быть составлено из бесконечного количества частей.
          3. Подобное же ошибочное заключение от невосприятия к несуществованию получается, при нежелании допустить то, что все конечные субстанции подлежат никогда не прекращающемуся изменению. На своей собственной душе мы достаточно знаем изменчивость ее состояний, представлений, свойств и сил; простая аналогия побуждает нас сделать подобное заключение о душах животных и о растениях. Но только основываясь на разуме мы в праве принять, что в действительности изменяются все субстанции, даже и те, которые в течение столетий не обнаруживают никаких заметных для нас изменений. Кто хочет оспаривать это, кто высказывается против этого, по крайней мере, в отношении так называемой мертвой материи и ее простых частей, или атомов, тот вынужден утверждать, что все изменения, являющиеся нам в этой части творения (если, например кусок льда, который был только что твердым, теперь растаял к в течение ближайшего часа улетучится в форме пара) – что все эти изменения (говорю я) суть перемены, касающиеся мест, занимаемых меньшими или большими частицами этих тел, при чем в самих частицах не происходить никаких внутренних перемен. Но как же можно не заметить противоречия в которое впадают при этом объяснении? В самом деле, если бы не происходило никакого изменения в простых субстанциях – внутри их, то в таком случае, что могло бы быть причиной перемен в отношении их мест, и какие следствия должны были бы иметь эти только внешние изменения, каковы были бы их цели и по каким признакам они могли бы быть хотя бы только узнаны? На все эти вопросы можно ответить разумно только в том случае, если признать, что простые субстанции, именно те, которые не совершенны, т.е. могут вместить большее количество сил, чем в них есть, по этому самому имеют способность к изменению при взаимодействии, и если рассматривать их места только как такие их определения, которые заключают основание, почему именно, владея данной мерой сил в данном промежутке времени, они вызывают одна в другой именно это, а не большее или меньшее изменение. Только при этом предположении, столь ясном и очевидном даже для обыкновенного человеческого ума, и исчезает всякое противоречие в учении о вселенной; нужно только подняться выше некоторых почти устарелых школьных мнений для признания того, что все находится в полном согласии.
Примечания
¹²) Dr. I. K. Fischer. Grundriss der gesammten hoheren Mathematik. Leipzig, 1809. Bd. II. § 51. Anm. назад к тексту12

¹³) pn = ap, pr = am,
     pr² = am² = ap² + pm² = pn² + pm²; pn² = pr² - pm².     Прим. ред.      назад к тексту13

¹⁴) mr = a - ((a² - dx)²)^1/2 = a - a(1 -(dx/a)²)^1/2.     Прим. ред.      назад к тексту14

¹⁵) Доказательство_этой истины столь кратко, что я позволю себе поместить его в этом примечании. Если линия amonb не прямая, то на ней должна находиться точка o, лежащая внe прямой ab и, если мы опустим перпендикуляр oω на ab, то расстояния удовлетворят неравенствам

aω < ao, bω < bo.

Но так как все системы двух точек подобны между собою, то между точками a и ω существует линия aμω, подобная той части amo данной линии amonb, которая лежит между точками a и o; между точками b и ω существует другая линия bνω, подобная той части bno данной линии bnoma, которая лежит между точками b и o. Но это подобие требует, чтобы длина прямой aω относилась к длине aμω так, как длина прямой ao к длине части amo, и чтобы длина прямой bω относилась к длине bνω так, как длина прямой bo к длине части bno. А так как aω < ao, то aμω < amo, и так как bω < bo, то и длина bνω должна быть меньше, чем bno. Следовательно, и целое aμωνb меньше целого amonb. Кривая линия amonb не будет, следовательно, кратчайшей линией между a и b, и кривая aμωνb будет короче ее.назад к тексту15

¹⁶) Гипербола не перемещается. Прим. ред. назад к тексту16